7.1. Олонлог логикийн элементүүд

Д.Хишигжаргал

А.Гантуул

Бага ангийн сурагчдыг математикийн хичээлээр хөгжүүлэхийн тулд онолын суурь ойлголт болох олонлог, түүн дээр хийгдэх үйлдлүүд, тэдгээрийн чанар, ангийн хуваалт, декарт үржвэр, төгсгөлөг олонлогийн элементийн тоо, нийлбэр ба үржвэрийн дүрэм, ухагдахуун, түүний агуулга, багтаамж, харьцаа, хэллэг, хэллэгжих хэлбэр, тэдгээрийн коньюнкц, дизьюнкц, үгүйсгэл, квантортой хэллэг, обьектуудын танин мэдэхүйн бодлогууд, өгүүлбэр хоорондын мөрдөн гарах ба тэнцүү чанарын харьцаа, теоремын бүтэц, түүний хэлбэр гэсэн онолын суурь ойлголтуудыг танин мэдэж, тэдгээртэй холбоотой асуудлыг олонлог дээр хийгдэх үйлдэл, тэдгээрийн чанаруудыг хэрэглэн шийдвэрлэхэд суралцана.

7.1.1.ОЛОНЛОГ

ХIХ зууны сүүл, ХХ зууны эхээр математикийн шинэ салбар болох олонлогийн онол бий болсон. Түүний үүсгэн байгуулагчийн нэг нь Германы математикч Георг Кантор юм.

Олонлог хэмээх ухагдахуун нь үндсэн ухагдахуун учир тодорхойлолтгүй хэрэглэдэг. Математикт нэгэн ижил зүйлүүдийг, эсвэл ялгаатай юмсыг нэг бүхэл болгон байнга судалдаг. Тухайлбал, натурал тоо, гурвалжин, квадрат, гэх мэт. Эдгээр бүх ялгаатай бөөгнөрлийг олонлог гэдэг. Нэг ч элемент агуулаагүй олонлогийг хоосон олонлог гэж нэрлээд \( \emptyset \) гэж тэмдэглэдэг.

Олонлогийг бүрдүүлж байгаа объектыг түүний элементүүд гэж нэрлээд, латин цагаан толгойн жижиг үсгээр тэмдэглэнэ. Энд: a, b, c, …z.

«а объект А олонлогт харьяалагдана» гэдгийг \( a \in A \) гэж тэмдэглэнэ. Харин «а объект А олонлогт харьяалагдахгүй» гэдгийг \( a \notin A \) гэж бичнэ.

Олонлогийг өгөх арга

Тодорхойлолт: Хэрэв В олонлогийн бүх элемент А олонлогийн элемент болж байвал В-г А олонлогийн дэд олонлог гэнэ. Хоосон олонлогийг дурын олонлогийн дэд олонлог болно. \( A \subset B \) ба \( B \subset A \) бол А, В олонлогуудыг тэнцүү олонлогууд гээд \( A = B \) гэж тэмдэглэнэ.

Видео 1. /5 мин/

Тодорхойлолт: А олонлогт ч, В олонлогт ч харьяалагдах элементүүдээс бүрдэх олонлогийг А ба В олонлогийн огтлолцол гэнэ. А ба В олонлогуудын огтлолцлыг \( A \cap B \) гэж тэмдэглэдэг. \( A \cap B = \{ x \mid x \in A \text{ ба } x \in B \} \).

Видео 2. /5 мин/

Тодорхойлолт: Зөвхөн А, эсвэл В олонлогт харьяалагдах элементүүдээс бүрдэх олонлогийг А ба В олонлогийн нэгдэл гэнэ. А ба В олонлогийн нэгдлийг \( A \cup B \) гэж тэмдэглэдэг. \( A \cup B = \{ x \mid x \in A \text{ эсвэл } x \in B \} \).

Тодорхойлолт: А олонлогт харьяалагддаг боловч, В олонлогт харьяалагддаггүй элементүүдээс зөвхөн бүрдэх олонлогийг А ба В олонлогуудын ялгавар гэнэ. А ба В олонлогийн ялгаврыг \( A \setminus B\) гэж тэмдэглэдэг. \( A \setminus B = \{ x \mid x \in A \text{ ба } x \notin B \} \) байна.

Тодорхойлолт: \( B \subset A \) байг. А-д харьяалагддаг ба В-д харьяалагддаггүй элементүүдээс зөвхөн бүрдэх олонлогийг В олонлогийн А олонлог хүртэлх гүйцээлт гээд \( \overline{B_A} \)гэж тэмдэглэнэ. \( B \subset A \) үед \( A \setminus B = \overline{B_A} \) болж, \( \overline{B_A} = \{x \mid x \in A \text{ ба } x \notin B\}\) байна.

Дүгнэлт

Энэ сэдэвт дараах ухагдахуунтай танилцсан. Үүнд:

• Олонлог, түүний элемент
• Олонлогийн элементийн тодорхойлох шинж
• Эх олонлог, дэд олонлог, хоосон олонлог, тэнцүү олонлог
• Олонлогуудын огтолцол, нэгдэл, ялгавар, гүйцээлт

Математикийн хэлээ дараах тэмдэглэгээгээр баяжуулав. Үүнд:

• \( а \in А, в \notin А \): («а-элемент А олонлогт харъяалагдана» ба «в-элемент А олонлогт харъяалагдахгүй» гэсэн өгүүлбэрийн бичлэг юм)
• \( A = \{1, 2, 3, 4\} \): (Олонлогийг түүний бүх элементийг тоочих аргаар өгсөн)
• \(A = \{x \mid x \in \mathbb{N} \text{ ба } x \leq 4\}\): (элементийн тодорхойлох чанараар олонлогийг өгсөн)
• \( А \cap В=\{ x \mid x \in A \text { ба } x \in В\}, А \cup В = \{ x \mid x \in A, \text { эсвэл } x \in В\}, А \setminus В =\{ x \mid x \in A \text { ба } x \notin В\}, \overline{B_A} = \{ x \mid x \in A \text { ба } x \notin В, B \subset A\}\) (А ба В олонлогийн огтолцол, нэгдэл, ялгавар, гүйцээлтийн тодорхойлолтын бичлэг)

7.1.2.Олонлогуудын декарт үржвэр

Тодорхойлолт: А ба В олонлогуудын декарт үржвэр гэж эхний координат нь А олонлогт харьяалагдах, хоёр дахь координат нь В олонлогт харьяалагдах бүх хосоос бүрдэх олонлогийг хэлнэ.

А ба В олонлогийн декарт үржвэрийг \(А\timesВ\) гэж тэмдэглэдэг. Энэ тэмдэглэгээг ашиглан декарт үржвэрийг \(А\timesВ = \{(x;y)\mid x \in A \text { ба } y \in В\}\) гэж бичиж болно.

Жишээ: Хэрэв а) \(A=\{m;p\}, B=\{e; f; k\};\) б) \(A=B=\{3;5\}\) бол А, В-ийн декарт үржвэрийг олоорой.

Бодолт: а) \(A \times B =\{(m; e), (m; f), (m; k), (p; e), (p; f), (p; k)\}\) байна. б) Өгөгдсөн олонлогуудын элементүүдээс бүх боломжит хосыг үүсгэж, тэнцүү олонлогуудын декарт үржвэрийг олбол: \(А \times A=\{(3; 3), (3;5), (5; 3), (5;5)\}\) болно.

Нэгдэл ба ялгаврын хувьд декарт үржвэр нь дистрибутив чанартай. Ө.х дурын А, В, С олонлогуудын хувьд:

1. \((A \cup B) \times C = (A \times C) \cup (B \times C)\)
2. \((A \setminus B) \times C = (A \times C) \setminus (B \times C)\) байна.

МАТЕМАТИКИЙН ӨГҮҮЛБЭР

Ярианы хэлний нэгэн адил математикт өөрийн тэмдэглэгээг хэрэглэн бодит үйл явцыг тодорхойлон бичдэг. Түүнийг өгүүлбэрүүдээр илэрхийлнэ. Тэгэхлээр бидний хүрээлэн буй бодит байдлыг зөв тусгасан математикийн мэдлэг нь бодит байхын тулд өгүүлбэрүүд үнэн зөв байх ёстой.

Үнэн ба худал мэдлэг математикийн өгүүлбэрээр хэрхэн илэрхийлэгдсэн байдгийг яаж мэдэх вэ? гэсэн асуулт урган гардаг .Энэ асуулт болон түүнтэй холбоотой бусад асуултанд номын §1.3 зүйлээр хариулахыг бид зорилоо. Харин математикийн өгүүлбэр бүр агуулга болон логик бүтэцтэй байх ба агуулга нь хэлбэртэйгээ тасралтгүй холбоотой. Энд логик бүтцийг ойлгохгүйгээр агуулгыг ухаарч мэдэх боломжгүй. Үүнтэй холбогдон «Логикийн элементүүд» бүлэгт математикийн өгүүлбэрийг судлахдаа математикийн өгүүлбэрийн логик бүтцийг нээн харуулахыг зорьсон.

Тодорхойлолт: Математикт үнэн, эсвэл худал утга санааг илэрхийлсэн хүүрнэх өгүүлбэрийг хэллэг гэнэ.

ХЭЛЛЭГИЙН КОНЪЮНКЦ БА ДИЗЪЮНКЦ

Тодорхойлолт: \(А\) ба \(В\) хэллэг нэгэн зэрэг үнэн үед үнэн, ядаж нэг нь худал байхад худал байдаг хэллэгийг \(А\) ба \(В\) хэллэгийн конъюнкц гээд \(А \land В\) гэж тэмдэглэдэг. Конъюнкцийн тодорхойлолтыг үнэний хүснэгт гэж нэрлэгдэх хүснэгтийн тусламжтайгаар бичвэл:

Тодорхойлолт: \(А\) ба \(В\) хэллэгүүдийн ядаж нэг нь үнэн байхад үнэн, хоёулаа нэгэн зэрэг худал үед худал байдаг хэллэгийг \(А\) ба \(В\) хэллэгийн дизъюнкц гээд \(А \lor В\) гэж тэмдэглэдэг. Дизъюнкцийн тодорхойлолтыг үнэний хүснэгт гэж нэрлэгдэх хүснэгтийн тусламжтайгаар бичвэл:

\(А\) ба \(В\) хэллэгийн конъюнкцийн үгүйсгэл нь тэдгээрийн үгүйсгэлийн дизъюнкц болохыг баталж болно. Үүний тулд \(\overline{A \land B}, \overline{A} \lor \overline{B}\) хэллэгийн үнэний утга \(А\) ба \(В\) хэллэгийн үнэний дурын утганд давхцахыг үзүүлэх хэрэгтэй. Үүнийг дараах үнэний утгын хүснэгтээр баталья. Үүнд:

Ерөнхий квантор (оршин байхын)-оор эхэлсэн хэллэгийн үгүйсгэлийг үүсгэхдээ оршин байх(ерөнхий)-ын квантороор солих ба кванторын дараах хэллэгийг үгүйсгэлээр нь солино.

Жишээ бодлого: «Нэг оронтой зарим тоонууд 10-д хуваагдана» гэсэн хэллэгийн үгүйсгэлийг үүсгээрэй.

Бодолт: Үүнийг 2 аргаар гүйцэтгэнэ.

1. Хэллэгийн төгсгөлд «... гэдэг нь худал» гэсэн үг бичнэ.Ингэснээр «Нэг оронтой зарим тоонууд 10-д хуваагдана гэдэг нь худал» гэсэн өгөгдсөн хэллэгийн үгүйсгэл үүснэ.
2. Оршин байхын квантор («зарим» гэсэн үгээр илэрхийлэгдсэн)-ыг, ерөнхий «бүх» гэсэн квантороор сольж, «зарим» гэсэн үгийн дараах өгүүлэхүүнийг (« ... гүй»

Өгүүлбэр хоорондын мөрдөн гарах ба тэнцүү чанарын харьцаа

Натурал тоонолонлог дээр «х-тоо 4-ийн хуваагдагч», «х-тоо 2-ын хуваагдагч» гэсэн хоёр хэллэгжих хэлбэрийг авч үзье.

Энэ хоёр өгүүлбэр өөр хоорондоо ямар холбоотой вэ?

х-тоо 4-ийн хуваагдагч гэдгээс х-тоо 2-ын хуваагдагч гэж мөрдөн гарна. Энэ нь «х-тоо 4-ийн хуваагдагч» байх бүх х-ийн утгад «х- тоо 2-ын хуваагдагч» гэсэн өгүүлбэр үргэлж үнэн байх учир батлагдаж байна. Энэ тохиолдолд өгөгдсөн өгүүлбэрүүдийг логик мөрдлөгөөний харьцаанд байна гэж ярьдаг.

Тодорхойлолт: Хэрэв В(х) хэллэгжих хэлбэрийн үнэн байх х-хувьсагчийн бүх утганд А(х) хэллэгжих хэлбэр үнэн байвал А(х) хэллэгжих хэлбэрээс В(х) хэллэгжих хэлбэр мөрдөн гарч байна гэнэ.

Хэрэв А хэллэг үнэн байхад В хэллэг үнэн байвал А хэллэгээс В хэллэгийг мөрдөн гарч байна гэнэ. Логикоор мөрдөн гарах харьцааг \(\Rightarrow\) гэж тэмдэглэдэг. \(А(х), В(х)\) хэллэгжих хэлбэрүүдийг тэр тэмдгээр холбож, \(А(х) \Rightarrow В(х)\) хэллэгийг гарган авч дараах байдлаар уншдаг. Үүнд:

1. А(х)-ээс В(х) мөрдөн гарч байна.
2. Ямарч А(х)-ийн хувьд В(х) биелнэ.
3. Хэрэв А(х) нь биелж байвал В(х) биелнэ.
4. В(х) нь А(х)-ийн мөрдлөгөө болно.
5. А(х) нь В(х)-ийн хүрэлцээтэй(хангалттай) нөхцөл юм.
6. В(х) нь А(х)-ийн гарцаагүй(зайлшгүй) нөхцөл юм.

Теоремийн бүтэц, түүний хэлбэрүүд

Ухагдахууныг логикоор судлахад математикт теорем гэж нэрлэгдэх өгүүлбэртэй холбоотой олон асуултыг нарийвчлан авч үздэг.

Тодорхойлолт: Эргэцүүлэн бодолтоор(баталгаагаар) үнэн болох нь илэрхийлэгдсэн хэллэгийг теорем гэнэ.

Логикийн үүднээс теорем нь нэг, эсвэл хэд хэдэн хувьсагчтай А,В хэллэгжих хэлбэрийн \(А \Rightarrow В\) дүрстэй хэллэг юм. А өгүүлбэрийг теоремын нөхцөл, харин В өгүүлбэрийг түүний дүгнэлт гэнэ.

Жишээ: «Хэрэв дөрвөн өнцөгт нь тэгш өнцөгт болж байвал түүний диагоналиуд тэнцүү байна» гэсэн теоремын нөхцөл нь «хэрэв дөрвөн өнцөгт нь тэгш өнцөгт болно», харин дүгнэлт нь «тэгш өнцөгт болно» өгүүлбэрүүд тус тус юм.

Энэ теорем «Хэрэв ... бол ...» үгийн тусламжаар томьёологдсон. Гэвч \(А \Rightarrow В\) өгүүлбэрийг өөрөөр томьёолж болно. Жишээ: «Ямарч тэгш өнцөгтийн диагоналиуд тэнцүү», эсвэл «дөрвөн өнцөгт тэгш өнцөгт байх зайлшгүй нөхцөл нь түүний диагоналиуд тэнцүү байх явдал» гэж өмнөх теоремыг томьёолж болно. Теоремыг томьёолох олон арга байдаг ч «Хэрэв ..... бол ...» үгийн тусламжаар томьёолох нь түүний нөхцөл ба дүгнэлт шууд харагддагаараа тохиромжтой.

Математикт теоремоос гадна дүрэм ба томьёо гэж нэрлэгдэх өгүүлбэрүүд хэрэглэдэг. Тэдгээрийн теоремоос ялгагдах онцлогийг авч үзье. Дунд сургуулийн алгебрийн курсээс «хэрэв \(a\)–дурын тоо, \(k\), \(n\)-натурал тоо байвал \(a^{n} \cdot a^{k} = a^{n+k}\) байдаг» теоремыг мэдэх билээ. Энэ теоремын нөхцөл нь «\(a\)- дурын тоо», «\(k\), \(n\)-натурал тоо» гэсэн өгүүлбэрүүд, харин дүгнэлт нь «\(a^{n} \cdot a^{k} = a^{n+k}\)» тэнцэтгэл болно. Үүнийг анхны өгсөн нөхцөлөөс үндэслэн батлах хэрэгтэй.

Дедуктив оюун дүгнэлтийн загварууд

Дедуктив(дүрмийн) оюун дүгнэлтийг дэлгэрүүлж авч үзье. Өмнөх сэдэвт тодорхойлсноор дедуктив оюун дүгнэлтийн илгээмж ба дүгнэлт логикоор мөрдөн гарах харьцаанд оршдог. Энэ нь түүний үнэн илгээмжээс үнэн дүгнэлт мөрдөн гарахыг илэрхийлж байгаа хэрэг. Гэвч тийм оюун дүгнэлтийг хэрхэн байгуулах ба тэдгээрийн үнэнийг хэрхэн шалгах вэ? гэсэн асуулт тавигддаг.

Логикт оюун дүгнэлтийн үнэн байдлыг түүний өгүүлбэрт оролцож байгаа өгүүлбэрийн агуулгаас үл хамааран хэлбэр тодорхойлдог. Логикийн тодорхой дүрмийг өгснөөр, дедуктив оюун дүгнэлтийг бүтээж болно. Тэдгээр дүрмийг гаргах дүрмүүд, эсвэл дедуктив оюун дүгнэлтийн загварууд гэж нэрлэдэг. Тэдгээр дүрэм олон байдагч хамгийн өргөн хэрэглэгддэг дараах дүрмийг авч үзье. Үүнд:

• \(\dfrac{A(x) \Rightarrow B(x),A(a)}{B(a)}\) -дүгнэх дүрэм,
• \(\dfrac{A(x) \Rightarrow B(x),\overline{B(a)}}{\overline{A(a)}}\) - үгүйсгэх дүрэм
• \(\dfrac{A(x) \Rightarrow B(x),B(x) \Rightarrow C(x)}{A(x) \Rightarrow C(x)}\) - дамжих дүрэм

\(Т_А, Т_В\) –нь \(А(х), В(х)\) хэллэгжих хэлбэрийн үнэний утгын олонлог үед \(A(x) \Rightarrow B(x)\) илгээмж \(Т_А \subset Т_В\) болно.

Тухайлсан \(А(а)\) гэсэн илгээмж нь \(а \in Т_А\) гэж тэмдэглэгдэх ба \(В(а)\) дүгнэлтийг \(а \in Т_В\) гэж харуулна.

Дүгнэх дүрмээр бүтээгдсэн бүх оюун дүгнэлт нь олонлогийн онолын хэл дээр \(\dfrac{T_A \subset T_B, a \in T_A}{a \in T_B}\) гэж бичигдэнэ.

\(Т_А, Т_В\) олонлогийг Эйлерийн диаграммаар дүрсэлж, \(а \in Т_А\) гэж тэмдэглэхэд \(а \in Т_В\) болох нь дараах зургаас шууд харагдана. Ө.х \(а \in Т_А \Rightarrow а \in Т_В\) болно.

Үүнтэй нэгэн адилаар дедуктив оюун дүгнэлтийн бусад дүрмийг баталж болно. Оюун дүгнэлтийн үнэнийг түүнээс өөр загвар ашиглах аргаар шалгаж болно.

Жишээ бодлого: «Хэрэв тооны бичлэг 5-аар төгсөж байвал, тэр тоо 5-д хуваагдана. 125 гэсэн тоо 5-д хуваагдана. Ингэхлээр 125 гэсэн тооны бичлэг 5-аар төгсөнө» гэсэн оюун дүгнэлт үнэн үү?

Бодолт: Энэ оюун дүгнэлтийг \(\dfrac{A(x) \Rightarrow B(x), B(125)}{A(125)}\) загвараар бичвэл түүний ерөнхий дүрс \(\dfrac{A(x) \Rightarrow B(x), B(a)}{A(a)}\) болно. Гэвч энэ загвар өмнө дурдсан загваруудаас өөр байна. Иймээс энэ нь дедуктив оюун дүгнэлтийн дүрэм болж чадах уу? гэсэн асуулт тавигдана.

Энэ асуултанд хариулахын тулд Эйлерийн диаграмм хэрэглэе. Гаргасан дүрмийг олонлогийн хэл дээр бичвэл \(\dfrac{Т_А \subset Т_В, а \in Т_В}{а \in Т_В}\) болно. Энд \(Т_А\) ба \(Т_В\) олонлогийг Эйлерийн диаграммаар дүрсэлж, \(Т_В\) олонлогт харьяалагдах элементийг а гэж тэмдэглэе. Гэвч тэр элемент \(Т_А\) олонлогт харьяалагдаж ч, харьяалагдахгүй ч байж болох нь дараах зурагт харагдаж байна.

Логикт ийм загварыг дедуктив оюун дүгнэлтийн дүрмээр тооцохгүй. Учир нь, түүний дүгнэлт зөв биш байна. Ер нь оюун дүгнэлтийг задлан шинжлэх үед оюун дүгнэлтийн үнэнийг гарган авсан дүгнэлтийн үнэнтэй адилсгаж болохгүй. Энд дүгнэлт нь үнэн байгаад оюун дүгнэлт өөрөө дедуктив биш, зөв биш байж болдог.

Өмнөх бодлогын хувьд түүгээр өгөгдөх оюун дүгнэлт зөв биш байна. Учир нь: Загвараар гүйцэтгэхэд дүгнэлт нь үргэлж үнэн байх боломжгүй байна.

Оюун дүгнэлт үнэн, эсвэл худал байгааг нотлохын тулд яах ёстой вэ? гэсэн асуулт тавигддаг. Үүнийг дараах 2 алхмаар гүйцэтгэнэ.

Нэгдүгээрт: өгөгдсөн оюун дүгнэлт өмнө гаргасан дүрмүүдийн аль нэг загварт тохирох, эсэхийг тогтоох

Хоёрдугаарт: өгөгдсөн оюун дүгнэлтийг олонлогийн онолын хэл дээр томьёолж, өмнөх бодлогынх шиг Эйлерийн диаграммаар дүрсэлнэ. Дүгнэх дүрэмтэй \(\dfrac{A(x) \Rightarrow B(x), B(a)}{A(a)}\) энэ загварыг, мөн үгүйсгэх дүрэмтэй\(\dfrac{A(x) \Rightarrow B(x),\overline{A(a)}}{\overline{B(a)}}\) загварыг сольж андуурахгүйн тулд эдгээрийг тогтооххэрэгтэй. Эдгээр загварууд нь үргэлж үнэн дүгнэлтгүй учир зөв дедуктив оюун дүгнэлт болж чадахгүй.

Квантортой хэллэг

Энэ зүйлд бид янз бүрийн хэлбэрийн математикийн өгүүлбэр судалсан. Тэдгээрээс энгийн болон нийлмэл хэллэг, хэллэгжих хэлбэрийг тодруулан тайлбарлаж, хэллэгийн үнэний утгыг, хэллэгжих хэлбэрийн үнэний утгын олонлогийг хэрхэн олох тухай мэдэж авсан. Гэвч математикийн өгүүлбэрийн олон янзын томьёоллыг, мөн тэдгээрийн дүрмийн хэрэглээг бүрэн авч үзээгүй. Жишээ: босоо өнцгийн тэнцүүгийн теоремыг олон янзаар томьёолдог. Үүнд:

Гүйцэд индукцийн оюун дүгнэлтийн загвар	Гүйцэд биш индукцийн оюун дүгнэлтийн загвар
\(х_1\)-элемент \(Р\) чанартай, \(х_2\)-элемент \(Р\) чанартай, \(х_3\)-элемент \(Р\) чанартай, ............................... \(х_n\)-элемент \(Р\) чанартай, \(х_1, х_2, х_3, …, х_n\)элементүүд Х олонлогийг бүрдүүлнэ.	\(х_1\)-элемент \(Р\) чанартай, \(х_2\)-элемент \(Р\) чанартай, \(х_3\)-элемент \(Р\) чанартай, ............................... \(х_n\)-элемент \(Р\) чанартай, \(х_1, х_2, х_3, …, х_n\)элементүүд Х олонлогт харъяалагдана.
Ингэхлээр \(Х\) олонлогийн элемент бүр \(Р\) чанартай байх нь баталгааны үр дүн болно.	Бидэнд үзэгдэж байгаагаар \(Х\) олонлогийн элемент бүр \(Р\) чанартай байх гэсэн батлах ёстой таамаглал өгүүлбэр байна.

• Босоо өнцгүүд хэмжээгээрээ тэнцүү байна.
• Хэрэв өнцгүүд босоо байвал тэдгээр өнцөг хоорондоо тэнцүү байна.
• Хэрэв А(х) нь биелж байвал В(х) биелнэ.
• Өнцгүүд хоорондоо тэнцүү байхын тулд тэдгээр нь босоо байх нь хангалттай.
• Өнцгүүд босоо байхын зайлшгүй нөхцөл нь тэд хэмжээгээрээ тэнцүү байх явдал юм.

Эсвэл «Гурван дурын дараалсан натурал тооны нийлбэр 3-д хуваагдана» гэсэн өгүүлбэр яагаад үнэн байгааг батлах, «Зарим натурал тоо 3-д хуваагддаг» гэсэн өгүүлбэрийн үнэнд итгүүлэхийн тулд тодорхой жишээ авах нь хангалттай юу? гэсэн асуултанд хариулахын тулд квантортой хэллэгийг гүнзгийрүүлэн судлах нь зайлшгүй юм.

Математикийн өгүүлбэрийн томъёололд «бүр», «бүх», «зарим нь», «ядаж нэг нь» гэсэн үг байнга тааралддаг. Жишээ: Тэгш өнцөгтийн эсрэг талын шинж чанарыг «Дурын тэгш өнцөгтийн эсрэг талууд хэмжээгээрээ тэнцүү» гэж томъёолдог. Натурал тооны чанарын тухай «Зарим натурал тоо 5-ын хуваагдагч» гэж ярьдаг. Эдгээр үг ямар утга санаатай байх, түүнийг математикт хэрхэн хэрэглэх тухай авч үзье.

Хэрэв хэллэгжих хэлбэр өгөгдсөн бол түүнийг хэллэгт шилжүүлэхдээ хувьсагчийн оронд нь тоо орлуулдаг. Жишээ: Хэрэв натурал тоон N олонлогт А(х)-«х-тоо 5-ын хуваагдагч» хэллэгжих хэлбэр өгөгдсөн бол х-ын оронд 20 гэсэн тоог орлуулахад «20-тоо 5-ын хуваагдагч» гэсэн үнэн хэллэг гарна. Хэрэв хэллэгжих хэлбэрт х-ын оронд 17-г орлуулахад «17-тоо 5-ын хуваагдагч» гэсэн худал хэллэг гарна.

Гэвч хэллэгжих хэлбэрээс хэллэг гаргах бусад өөр аргууд ч байдаг.

Хэрэв «х-тоо 5-ын хуваагдагч» гэсэн өмнөх хэллэгжих хэлбэрийн өмнө «ямар ч» гэсэн үг тавивал «Ямар ч х-тоо 5-ын хуваагдагч» гэсэн өгүүлбэр гарна. Энэ өгүүлбэрийн хувьд үнэн, эсвэл худал байх уу? гэсэн асуулт тавигдана. Тэгвэл «Ямар ч х-тоо 5-ын хуваагдагч»\((x \in \mathbb{N})\) гэсэн өгүүлбэр худал хэллэг байна.

Логикт «Ямар ч х-ын хувьд» гэсэн илэрхийллийг х-хувьсагчтай ерөнхийллийн квантор (хувьсагчийг өөр үсгээр тэмдэглэсэн байж болно) гэж нэрлээд \(\forall х\) гэж тэмдэглэдэг.

\((\forall х)\) нь \(А(х)\) бичлэг нь «х-ын ямарч утганд \(А(х)\) өгүүлбэр үнэн хэллэг» байхыг тэмдэглэнэ. Заримдаа энэ бичлэгт \(Х\) олонлогийг нэмж, \((\forall х \in Х)\) бол \(А(х)\) өгүүлбэрийг дараах байдлаар уншдаг.Үүнд:

a) \(Х\) олонлогийн ямар ч \(х\)-ийн хувьд \(А(х)\) үнэн байна.

b) \(Х\) олонлогийн ямар ч \(х\)-элемент \(А\) чанарыг агуулна.

Логикт « .... байх \(х\) оршин байна» гэсэн илэрхийллийг х-хувьсагчтай оршин байхын квантор (хувьсагчийг өөр үсгээр тэмдэглэсэн байж болно) гэж нэрлээд \(\exists х\) гэж тэмдэглэдэг.

(\(\exists х\)) \(А(х)\) бичлэг нь «\(А(х)\) өгүүлбэрийг үнэн хэллэг болгох х-хувьсагчийн утга оршин байна» гэдгийг тэмдэглэнэ. Заримдаа энэ бичлэгт \(Х\) олонлогийг нэмж, (\(\exists х \in Х\)) \(А(х)\) өгүүлбэрийг дараах байдлаар уншдаг.Үүнд:

a) \(Х\) олонлогоос \(А(х)\)-ийг үнэн хэллэг болгох \(х\) оршин байна.

b) \(Х\) олонлогийн ядаж нэг \(х\)-элемент нь \(А\) шинж чанарыг агуулна.

Обьектуудын танин мэдэхүйн бодлого бодох

Хэллэгжих хэлбэрийн конъюнкц, дизъюнкцийн ухагдахуун оруулснаар обьектуудыг танин мэдэх бодлого гэж нэрлэгдэх тодорхой хэлбэрийн бодлогын бодолттой холбоотой асуултууд авч үзэх боломжийг бүрдүүлдэг.

Танин мэдэхүйн бодлогод тухайн обьект өгөгдсөн ухагдахуунд багтаж байна уу?, эсвэл багтахгүй байна уу? гэсэн асуултад хариулдаг. Жишээ: Дараах зургийн дүрсүүдээс аль нь квадрат болох, болохгүйг тодорхойл” гэсэн бодлого байна.

Ийм бодлого бодоход харгалзах ухагдахууны тодорхойлолтыг хэрэглэнэ. Хэрэв \(a\)–ухагдахууныг \(C\)–төрлийн ухагдахуун болон \(Р\) – хэлбэрийн онцлогоор тодорхойлсон үед түүний \(A\) багтаамжийг \(A=\{x \mid x \in С \text { ба } Р(x)\}\) гэж бичдэг. Энэ бичлэг нь \(a\)-ухагдахууны \(A\) багтаамжийн элементүүдийн тодорхойлох чанарыг хоёр чанарын конъюнкцоор илэрхийлж байна. Үүнд:

1. \(х\)-обьект нь төрөл ухагдахууны \(С\) багтаамжид харьяалагдана(\(х \in С\)).
2. \(Р(х)\) шинж чанартай.

Үүгээр "\(х\)-обьект нь \(а\)-ухагдахууны багтаамжид харьяалагдах зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь төрөл ухагдахууны багтаамжид харьяалагдахаас гадна, \(Р\) шинж чанарыг агуулах явдал юм" гэснийг илэрхийлнэ. Иймээс обьектийн танин мэдэхүйг дараах дүрмээр гүйцэтгэнэ. Үүнд:

1. \(x\)-обьект төрөл ухагдахууны багтаамжид орж байгаа эсэхийг ө.х \(x \in C\) хэллэг үнэн, эсэхийг шалгана.
2. Хэрэв \(x \notin C\) байвал, \(x\)-обьект \(a\)-ухагдахууны багтаамжид орохгүй гэсэн дүгнэлтэнд хүрнэ. Ө.х \(x \notin A\).
3. Хэрэв \(x \in C\) байвал \(x\)-обьект \(P\) шинж чанарыг агуулсан, эсэхийг шалгана.
4. Хэрэв \(x\)-обьект \(Р\) шинж чанарыг хангаж байвал \(a\)-ухагдахууны багтаамжид харьяалагдаж байгаа дүгнэлт гаргана. Ө.х \(x \in А\) гэж баталж байгаа хэрэг.
5. Хэрэв \(x\)-обьект \(P\) шинж чанарыг хангахгүй байвал \(a\)-ухагдахууны багтаамжид \(x\)-обьект харьяалагдахгүй байгаа дүгнэлт гаргана. Ө.х \(x \notin A\) байна.

Өгүүлбэр хоорондын мөрдөн гарах ба тэнцүү чанарын харьцаа

Натурал тоонолонлог дээр «х-тоо 4-ийн хуваагдагч», «х-тоо 2-ын хуваагдагч» гэсэн хоёр хэллэгжих хэлбэрийг авч үзье.

Энэ хоёр өгүүлбэр өөр хоорондоо ямар холбоотой вэ?

х-тоо 4-ийн хуваагдагч гэдгээс х-тоо 2-ын хуваагдагч гэж мөрдөн гарна. Энэ нь «х-тоо 4-ийн хуваагдагч» байх бүх х-ийн утгад «х- тоо 2-ын хуваагдагч» гэсэн өгүүлбэр үргэлж үнэн байх учир батлагдаж байна. Энэ тохиолдолд өгөгдсөн өгүүлбэрүүдийг логик мөрдлөгөөний харьцаанд байна гэж ярьдаг.

Тодорхойлолт: Хэрэв \(B(x)\) хэллэгжих хэлбэрийн үнэн байх \(x\)-хувьсагчийн бүх утганд \(A(x)\) хэллэгжих хэлбэр үнэн байвал \(A(x)\) хэллэгжих хэлбэрээс \(B(x)\) хэллэгжих хэлбэр мөрдөн гарч байна гэнэ.

Хэрэв \(A\) хэллэг үнэн байхад \(B\) хэллэг үнэн байвал \(A\) хэллэгээс \(B\) хэллэгийг мөрдөн гарч байна гэнэ. Логикоор мөрдөн гарах харьцааг \(\Rightarrow\) гэж тэмдэглэдэг. \(A(x), B(x)\) хэллэгжих хэлбэрүүдийг тэр тэмдгээр холбож, \(A(x) \Rightarrow B(x)\) хэллэгийг гарган авч дараах байдлаар уншдаг. Үүнд:

1. \(A(x)\)-ээс \(B(x)\) мөрдөн гарч байна.
2. Ямарч \(A(x)\)-ийн хувьд \(B(x)\) биелнэ.
3. Хэрэв \(A(x)\) нь биелж байвал \(B(x)\) биелнэ.
4. \(B(x)\) нь \(A(x)\)-ийн мөрдлөгөө болно.
5. \(A(x)\) нь \(B(x)\)-ийн хүрэлцээтэй(хангалттай) нөхцөл юм.
6. \(B(x)\) нь \(A(x)\)-ийн гарцаагүй(зайлшгүй) нөхцөл юм.

Жишээ: «х-тоо 4-ийн хуваагдагч» гэсэн өгүүлбэрээс «х-тоо 2-ын хуваагдагч» гэсэн өгүүлбэр мөрдөн гарч байгааг дараах байдлаар томьёолж болно. Үүнд:

• 4-ийн хуваагдагч ямарч тоо 2-ын хуваагдагч байна.
• Хэрэв тоо 4-ийн хуваагдагч болж байвал 2-ын хуваагдагч болно.
• 2-ын хуваагдагч нь түүний 4-ийн хуваагдагчаас мөрдөн гарна.
• 4-ийн хуваагдагч нь 2-ын хуваагдагч байхын хүрэлцээтэй нөхцөл юм.
• 2-ын хуваагдагч нь 4-ийн хуваагдагч байхын гарцаагүй нөхцөл юм.

Эдгээрийн сүүлчийн хоёр өгүүлбэрийг дараах байдлаар томьёолж болно. Үүнд:

• 2-ын хуваагдагч байхын хүрэлцээтэй нөхцөл нь 4-ийн хуваагдагч байх явдал.
• 4-ийн хуваагдагч байхын гарцаагүй нөхцөл нь 2-ын хуваагдагч байх явдал

«\(A(x)\)-ээс \(B(x)\) мөрдөн гарна» гэсэн нэг өгүүлбэрийг олон янзаар уншиж байгаа учир тэдгээрийг өөр хооронд нь утга алдагдуулахгүйгээр шилжүүлэн томьёолох чадвар хэрэгтэй.

Жишээ бодлогууд

Бодлого 1: Өгөгдсөн өгүүлбэрүүдийг \(A(x)\) \(B(x)\) өгүүлбэр унших олон хувилбар хэрэглэн томьёол.
а) Ямарч квадрат тэгш өнцөгт болдог.
б) Тоо 5-д хуваагдахын хүрэлцээтэй нөхцөл нь тэр тооны аравтын тооллын системийн бичлэг тэгээр төгсөх явдал юм.

Бодолт: а) Өгсөн хэллэгээс 2 өгүүлбэрийг ялгаж авч болно. Үүнд: \(A(x)\)-«Дөрвөн өнцөгт нь квадрат» ба \(B(x)\)-«Дөрвөн өнцөгт нь тэгш өнцөгт». Тэдгээр нь « Ямарч» гэсэн үгтэй өгүүлбэрээр илэрхийлэгдсэн мөрдөн гарсан \(A(x) \Rightarrow B(x)\) гэсэн харьцаанд оршино. Өгөгдсөн хэллэгийг дараах байдлаар өөрчлөн томьёолж болно. Үүнд:

1. Дөрвөн өнцөгт квадрат гэдгээс тэгш өнцөгт байна гэж мөрдөн гарна.
2. Хэрэв дөрвөн өнцөгт квадрат байвал тэгш өнцөгт болно.
3. Дөрвөн өнцөгт тэгш өнцөгт байх нь дөрвөн өнцөгт квадрат гэдгийн мөрдлөгөө юм.
4. Дөрвөн өнцөгт тэгш өнцөгт байхын хүрэлцээтэй нөхцөл нь квадрат байх явдал юм.
5. Дөрвөн өнцөгт квадрат байхын зайлшгүй нөхцөл нь тэгш өнцөгт байх явдал юм.

б) Өгөгдсөн хэллэгийг а) шиг хоёр өгүүлбэрт задалж болно. Үүнд: \(P(x)\)-«Тоо 5-д хуваагддаг» ба \(K(x)\)-«Тооны бичлэг тэгээр төгсөнө». 2 дугаар өгүүлбэр нь 1 дүгээр өгүүлбэрийн хүрэлцээтэй нөхцөл болно. Иймээс энд биелэх мөрдөн гарах \(P(x) \Rightarrow K(x)\) харьцааг дараах байдлаар томъёолж болно. Үүнд:

1. Тооны бичлэг тэгээр төгсөхөөс тэр тоо 5-д хуваагдах нь мөрдөн гарна.
2. Бичлэг тэгээр төгссөн ямарч тоо 5-д хуваагдана.
3. Хэрэв тооны бичлэг тэгээр төгсөж байвал тэр тоо 5-д хуваагдана.
4. Тоо 5-ын хуваагдагч байх нь түүний бичлэг тэгээр төгсөхийн мөрдлөгөө болно.
5. Тооны бичлэг тэгээр төгсөж байвал тэр тоо 5-д хуваагдах нь зайлшгүй нөхцөл юм.

Ямарч хэллэг шиг \(A(x) \Rightarrow B(x)\) өгүүлбэр үнэн, эсвэл худал байна. Гэвч түүнийг «Ямарч \(A(x)\) биелэх үед \(B(x)\) биелнэ» гэж томъёолох учир түүний үнэнийг нь батлах замаар, харин худлыг нь няцаах жишээгээр харуулдаг.

Бодлого 2: Дараах хэллэгийн үнэний утгыг тодорхойл.
а) Хэрэв тооны бичлэг 6-аар төгсөж байвал тэр тоо 2-д хуваагдана.
б) Тоо 5-д хуваагдахын зайлшгүй нөхцөл нь түүний бичлэг тэгээр төгсөх явдал юм.

Бодолт: а) Энэ хэллэг илэрхий үнэн. Үнэхээр бичлэг нь 6 гэсэн цифрээр төгссөнямарч тоо тэгш тоо байдаг. Ямарч тэгш тоо 2-д хуваагдана. Ингэхлээр 6 цифрээр төгссөн тоо 2-д хуваагдана. Энэ хэллэгийн үнэнийг бид баталлаа.

б) Хэрэв өгсөн хэллэгийг «Тоо 5-д хуваагдана гэдгээс тэр тооны бичлэг тэгээр төгсөнө» гэсэн хэлбэрээр томьёолбол шууд худал хэллэг болно. Түүнийг жишээгээр няцааж харуулна. Тухайлбал, 35 гэсэн тоо 5-д хуваагдах боловч, түүний бичлэг тэгээр төгсөхгүй.

Хэрэв \(A(x)\) хэллэгжих хэлбэрийн үнэний олонлогийг \(Т_А\), \(B(x)\) хэллэгжих хэлбэрийн үнэний олонлогийг \(Т_В\) гэж тэмдэглэвэл, олонлогийн онолын үүднээс \(A(x) \Rightarrow B(x)\) хэллэг нь \(Т_А \subset Т_В\) байна. Урвуу өгүүлбэр нь үнэн байна.

Үүнийг заримдаа \(A(x) \Rightarrow B(x)\) хэллэгийн үнэний утгыг тодорхойлоход хэрэглэхэд тохиромжтой байдаг.

Бодлого 3: Бүхэл тоон олонлог дээр \(3x(x-2)=0\) тэгшитгэлээс \(3x(x-2)(x+3)=0\) тэгшитгэл мөрдөн гарахыг батал.

Бодолт: 1 дүгээр тэгшитгэлийн шийдийн олонлог \(T_1 =\{0;2\}\), 2 дугаар тэгшитгэлтийн шийдийн олонлог \(T_2 =\{0;2;-3\}\) учир \(T_1 \subset T_2\) байна. Иймээс \(3x(x-2)=0\) тэгшитгэлээс \(3x(x-2)(x+3)=0\) тэгшитгэл мөрдөн гарна.

\(A(x)\): «Тоо 3-д хуваагддаг» ба \(B(x)\): «Тооны цифрүүдийн нийлбэр 3-д хуваагддаг» гэсэн хоёр хэллэгжих хэлбэрийг авч үзье. Дунд сургуулийн математикийн курсээс "Хэрэв тоо 3-д хуваагдаж байвал түүний цифрүүдийн нийлбэр 3-д хуваагдана", түүний урвуу өгүүлбэр үнэн байдгийг мэднэ. Энэ үед \(A(x)\) ба \(B(x)\) өгүүлбэрүүдийг харилцан тэнцүү чанартай гэдэг.

Тодорхойлолт: Хэрэв \(A(x)\) өгүүлбэрээс \(B(x)\) өгүүлбэр мөрдөн гардаг, мөн \(B(x)\) өгүүлбэрээс \(A(x)\) өгүүлбэр мөрдөн гарч байвал \(A(x), B(x)\) өгүүлбэрүүдийг харилцан тэнцүү чанартай гэнэ.

Асуулт даалгавар

1. Зургийг ажиглаад олонлогуудын ямар харьцаанд оршин байгааг нэрлээрэй.
2. Дараах олонлогийн элементүүдийг тоочин бичээрэй.
   1. М нь нэг оронтой сондгой тооны олонлог
   2. К нь 5-аас бага натурал тооны олонлог
   3. Р нь 2-оос их 9-өөс бага натурал тооны олонлог
   4. S нь 10-д хуваагддаг хоёр оронтой тооны олонлог
   5. R нь -3-аас их 3.7-оос бага бүхэл тооны олонлог

Ашигласан ном зүй:

1. Магсар, Р., Энхцэцэг, Д., Балдулмаа, Б., Нямжав, Ц., Мөнхжаргал, М., Мягмарсүрэн, Ө., Хадбаатар, Б., & Амартүвшин, Д. (2012). Бага боловсролын математикийн онол. УБ: Бит пресс.
2. Магсар, Р., Энхцэцэг, Д., Балдулмаа, Б., Нямжав, Ц., Мөнхжаргал, М., Мягмарсүрэн, Ө., Хадбаатар, Б., & Амартүвшин, Д. (2013). Бага боловсролын математикийн онолын бодлогын хураамж. УБ: Бит пресс.
3. Балдулмаа, Б., Нямжав, Ц., Энхцэцэг, Д., Норов, С., Мөнхжаргал, М., Чулуунцэцэг, О., Мягмарсүрэн, Ө. (2010). Бага боловсролын математикийн онол, дидактик. УБ: Интерпресс.
4. Норов, С. (2010). Бага боловсролын математикийн онолын мэдлэг шалгах сэдвүүд. УБ.
5. Магсар, Р., Амартүвшин, Д., Хадбаатар, Б., & Хишигжаргал, Д. (2018). Бага боловсролын математикийн онол. УБ: Бит пресс.
6. C.A.R. Bailey. Sets and logic 1. London: Western printing services LTD.
7. Herbert B. Enderton. (2009). Elements of set theory. Academic Press.
8. https://www.youtube.com/watch?v=mKvNZlbZKWU
9. https://www.youtube.com/watch?v=xZELQc11ACY
10. https://www.youtube.com/watch?v=9R9QQoFH-p8
11. https://www.youtube.com/watch?v=H5D6EAezsXQ
12. https://www.youtube.com/watch?v=5ZhNmKb-dqk

7.2. ГЕОМЕТР БА ХЭМЖИГДЭХҮҮН СУРГАЛТЫН АРГА ЗҮЙ

Б.Хадбаатар

7.2.1.Цэг, шулуун, хэрчим, тахир шугам, олон өнцөгт

Бага ангид геометрийн материалыг судлах үндсэн зорилго нь цэг, шулуун шугам, шулууны хэрчим, тахир шугам, өнцөг, олон өнцөгт дугуй зэрэг геометрийн дүрсийн тухай анхны ухагдахуун ба тэдгээрийн тодорхой төсөөллийг сурагчдад төлөвшүүлэх явдал юм.

Үүнд ажиллуулах дасгал, геометрийн агуулгатай бодлого, түүн дээр ажиллах арга зүйн систем нь хүүхдийн ажиглах, жиших, хийсвэрлэх, нэгтгэн дүгнэх чадвар, орон зайн төсөөллийг хөгжүүлэхэд чухал үүрэг гүйцэтгэнэ. Сургалтын бас нэг зорилго нь

• Нүдэн баримжаагаар хэмжин гараар зурах
• Гортиг, шугам, транспортир ашиглан геометрийн дүрсүүдийг зурах, хэмжих, байгуулах зэрэг практик чадвар олгох явдал юм

Түүнчлэн хэмжих байгуулах ажлыг нарийн дэс дараалалтай гүйцэтгэх анхны төсөөлөлтэй болно. Хөтөлбөрт тусгасан геометрийн материалыг судлахын тулд бодлого, дасгалыг гүйцэтгүүлэхдээ төрөл бүрийн үзүүлэн таниулах материал ашиглах нь илүү үр дүнтэй. Анги нийтээр үзүүлэх хэрэглэгдэхүүний хувьд өнгийн хатуу цаас болон пластик материалаар бэлтгэсэн геометрийн дүрсийн загварууд, цахим үзүүлэн, самбарт зурсан график зураг, геометрийн дүрс зэрэг байж болно. Түүнээс гадна янз бүрийн савх мод, баримлын шавар, өнгийн цаас, цаасаар хайчилсан дүрс, зэрэг тарааж өгөх материалууд бэлтгэх нь чухал. Зарим сэдвийг судлахдаа өнцгийн загвар, өнцгийн эвхмэл загвар (малка) (зураг. 1), палеткa (зураг. 2) талбайг хэмжих нэгжийн загвар гэх хэрэглэгдэхүүн ашиглаж болно. Самбарт зурж хэмжихэд зориулсан багшийн багажны иж бүрдэл, сурагчид ашиглах гортиг, шугамны иж бүрдэлтэй байх ёстой.

Геометрийн материалыг таниулахдаа практик үйл ажиллагаанд тулгуурлан явуулбал илүү үр дүнтэй. Үүнд: Цаас, савх мод, утас, баримлын шавар ашиглан дүрс, биетийн загвар бүтээх, хэмжилт хийх, зурах г.м. Өнгө, хэмжээ, байрлал зэрэг гол биш шинж чанарууд нь янз бүрээр өөрчлөгдөж байх төрөл бүрийн дүрс болон биетүүдийг сурагчдад өгч эдгээрийн үндсэн шинж чанаруудыг төстэй болон ялгаатай байдлаар нь ялгаж ойлгож авахад туслах хэрэгтэй. Математикийн ухагдахуунуудыг судалж байх үедээ өмнө үзсэн геометрийн материалтай уялдуулж болох бүхий л боломжийг эрж хайвал зохино.

Дүгнэлт

• Нэг цэгийг дайруулж хэчнээн ч шулуун татаж болно.
• Нэг цэгийг дайруулж хэчнээн ч тахир шугам татаж болно.
• Хоёр цэгийг дайруулан зөвхөн ганц шулуун татаж болно.
• Хоёр цэгийг дайруулан хэдэн ч муруй шугам татаж болно гэх мэт.
• Аливаа графын хувьд түүний бүх оройн зэргийн нийлбэр тэгш байх бөгөөд графын ирмэгийн тоог 2 дахин авсантай тэнцүү байна.
• Аливаа графын сондгой оройнуудын тоо тэгш байна.
• Биетийн хувьд O+T-И=2 нөхцөл биелнэ.
• Зөвхөн хоёр сондгой орой бүхий графыг ганц зуралтаар зурж болох ба тэгэхдээ энэ хоёр сондгой оройн аль нэгээс эхэлж нөгөө дээр нь төгсөнө.
• Мөн граф нь нэг ч сондгой орой агуулаагүй бүх орой нь тэгш бол түүнийг нэг удаагийн зуралтаар зурж болно.

7.2.2.Граф гэж юу вэ?

Графын онолын үүсэл

XX зууны эхэн үеэс графын онол математикийн бие даасан нэгэн салбар болж хөгжиж, одоо үед автомат удирдлага, телемеханик, кибернетик, электроник, физик болон шинжлэх ухааны бусад салбарт өргөн хэрэглэгдэх болсон.

Түүхэн бодлого: Эртний Кенигсберг одоогийн Калининград хотын дундуур Прегель гол хотын дундуур урсдаг. Кенигсбергийн оршин суугчдад бүх гүүрээр зөвхөн нэг удаа дамжин өнгөрөх боломжтой юу гэсэн асуудал дэвшигдэж байсан бөгөөд түүнийг онолын хувьд болон практик дээр шийдэж чадалгүй олон жил өнгөрчээ. Харин 1736 онд алдарт математикч Леонард Эйлер (1707-1783) энэхүү асуудлыг шийдээд зогсохгүй ерөнхий тохиолдолд графын тухай онолын үндэслэлийг дэвшүүлсэн байдаг.

“Долоон гүүрний “ тухай бодлогыг Эйлер дараах байдлаар томьёолон боджээ.

Tэp В, С цэгүүдээр эргүүдийг, A, D цэгүүдээр голын эрэг ба арлуудыг холбосон гүүрнүүдийг шугамуудаар дүрсэлжээ. Энэ дүрсийг граф гэж нэрлэх ба A,B,C,D цэгүүдийг графын оройнууд, энэ оройнуудыг холбосон муруйг графын нум / буюу ирмэг / гэнэ.

Эйлер энэ графын орой бүрээс гарсан нумын тоог тооцоолж үзсэн. В,С, D орой тус бүрээс гурав, харин А оройгоос таван нум гарсан байна. Графын ямар нэг оройгоос сондгой тооны нум гарсан байвал түүнийг сондгой орой, хэрэв түүнээс тэгш тооны нум гарсан байвал түүнийг тэгш орой гэж тэр нэрлэжээ. Хэрэв бүх оройн зэрэг тэнцүү бол уул графыг нэгэн төрлийн граф гэж нэрлэдэг. Хэрэв хөдөлгөөн А оройгоос эхлэн графийн хэд хэдэн оройнуудыг дайран өнгөрөхдөө ирмэг бүрийн дагуу зөвхөн 1 удаа дайрч уул А орой дээрээ эргэн ирсэн байвал тийм замыг цикл гэж нэрлэнэ. Ерөнхийдөө дурын битүү гинж бүрийг цикл гэж нэрлэнэ.

Ямар ч графыг зурж болох боловч хамгийн цөөн зуралтын тоо нь уул графын сондгой оройнуудын тооны хагастай тэнцүү байна.

Дунд сургууль төгсч байгаа 4 сурагч фото зургаа солилцох болжээ. Сурагч нэг бүрд түүний нэрний эхний үсгээр тэмдэглэсэн хавтгайн тодорхойн нэгэн цэгийг харгалзуулан. тэдгээрийг хэрчим буюу нумаар зураг солилцсоныг тэмдэглэе.

А, Б, В, Г ,Д цэгүүдийг графын оройнууд гэж нэрлэх ба харин цэгүүдийг холбосон шугамуудын / шулуун шугам эсвэл муруй шугамын хэсгүүдийг графын ирмэгүүд гэдэг. Энэ зурагт зөвхөн цэгүүд дүрсэлсэн нь фото зураг солилцож эхлээгүй байгааг харуулж байна. Энэ цэгэн схемийг холбоост биш /тэг/ граф гэнэ. Өөрөөр хэлбэл тэг граф нь саланги оройнуудаас тогтоно.

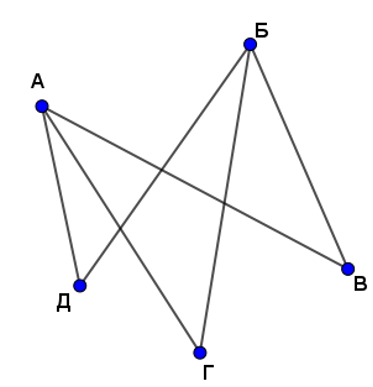
Ийм графыг гүйцэт хобоост граф гэнэ. Энэ графын А, B, C, D, E цэгүүдийг холбосон шугамууд эдгээр цэгүүдээс өөр огтлолцлын цэггүй байхаар дүрсэлж болно. Хэрэв графын ирмэгүүд нь зөвхөн оройнууд дээрээ л огтололцохоор хавтгай дээр зурж болох графыг хавтгай граф гэж нэрлэнэ. Иймд зураг 3 дээрх графыг хавтгай граф гэнэ. Энэ графыг түүний оройнуудын хавтгай дээрх байрлалыг өөрчилж өөр байдлаар зурж болно.

Дээрх 3 зураг дээрх графууд нь тухайн бодлогын шийдийн талаар нэг л ижил мэдээлэл өгнө. Иймээс эдгээр графыг ижил буюу изоморф графууд гэнэ.

Фото зургаа бүгд солилцсон байдалд дараах зураг дээрх граф харгалзана. Энэ граф нь гүйцэд граф болно.Хэрэв графын дурын хоёр орой бүхэн ирмэгээр холбогдсон байвал түүнийг гүйцэд граф гэнэ. Бага ангийн математикийн сургалтад д үрсийг ганц удаагийн зуралтаар зурах боломж тоолох бодлого зэрэгт графыг ашиглаж болно.

Дүгнэлт

• Аливаа графын хувьд түүний бүх оройн зэргийн нийлбэр тэгш байх бөгөөд графын ирмэгийн тоог 2 дахин авсантай тэнцүү байна.
• Аливаа графын сондгой оройнуудын тоо тэгш байна.
• Зөвхөн хоёр сондгой орой бүхий графыг ганц зуралтаар зурж болох ба тэгэхдээ энэ хоёр сондгой оройн аль нэгээс эхэлж нөгөө дээр нь төгсөнө.
• Мөн граф нь нэг ч сондгой орой агуулаагүй бүх орой нь тэгш бол түүнийг нэг удаагийн зуралтаар зурж болно.

7.2.3.Хялбар байгуулах бодлогууд

Нэгдүгээр ангид анхны аравтыг үзэж байх үед геометрийн дүрсийг дидактикийн материал болгон ашигладаг. Үүнд тулгуурлаж сурагчид тоолох, бодлого бодох, тооцоолон бодох, хээ угалз зохиох, дүрсийн зохиомж хийх, жиших, ажиглах ажлыг хийж сурдаг. Үүний зэрэгцээгээр дүрс бүрийн тухай төсөөлөл нарийвчлагдаж, дүрсийн нэртэй танилцана. Жишээ нь: дугуй, гурвалжин, квадрат гэх мэтээр ялгаж чаддаг болно. Дараагийн шатанд олон өнцөгтийн хэлбэрүүдийг тусгайлан авч үзнэ.

Үүний хамт олон өнцөгтийн элементүүдийг тал, өнцөг, орой гэх мэт ялгана. Тухайлбал 3-ын тоог үзэж байх үед янз бүрийн хэлбэртэй гурвалжинтай танилцана. Энэ үед хүүхэд өнгийн цаас, баримлын шавар, савх модоор хийсэн гурвалжны загвараар ажиллаж дүрс тус бүрийн гурван тал, гурван орой, гурван өнцгийг зааж сурна. Мөн нэрлэж сурна. Дараа нь хүүхдүүд өөрсдөө савх мод, баримлын шавар, цаасаар гурвалжин дүрс хийнэ. Мөн оройг цэгээр тэмдэглэнэ. Гурвалжныг зурж будна. Гурвалжин хэлбэр дүрстэй зүйлс нэрлүүлэх, самбарт зурсан буюу цуглуулсан дүрс дотроос гурвалжныг олуулах дасгал ажиллуулна. Харин цуглуулгандаа янз бүрийн өнцөгтэй гурвалжинг авах нь чухал. Энэ үед гурвалжны тухай зөв төсөөллийг төлөвшүүлэхэд тусална. Олон өнцөгтийн элементүүдийг ялгаснаар тухайн дүрсийн нэр ба элементийн тоо хоёрын хоорондох холбоонд анхаарлаа хандуулна.

Гурвалжинд гурван тал, гурван орой, гурван өнцөг; дөрвөн өнцөгтөд-дөрвөн тал, дөрвөн орой, дөрвөн өнцөг байдаг гэх мэт. Мөн тухайн олон өнцөгтийн өнцөг, орой, тал нь ижил тоотой байдгийг ухамсарлана. Энэ бүх мэдлэгийг чадварыг сурагчид бэлэн загвар ажиглах буюу олон өнцөгтийг зурах, эвлүүлэх, хэмжих гэх мэт практик дасгалын явцад олж авна. Зөвхөн тэнцүү талтай олон өнцөгтийг ажиглуулахгүйн тулд элдэв загвар бүтээхэд уртаараа янз бүрийн хэмжээтэй тууз цаас буюу савх мод зэргийг ашиглах нь илүү тустай гэдгийг санах хэрэгтэй.

Дүгнэлт

Зөв олон өнцөгтийн хувьд:
• Бүх талууд болон оройн өнцгүүд тэнцүү
• Талуудынхаа тоотой тэнцүү тэгш хэмийн тэнхлэгтэй
• Багтсан ба багтаасан тойргийн төвүүд давхцдаг
• Дотоод өнцгүүдийн нийлбэр (n-2)x180
• Нэг орой дах өнцгийн хэмжээ (n-2)x180/n

Асуулт даалгавар

7.3. Бага боловсролын байгалийн ухааны үндэс

Ш.Дауренбек

Б.Баярчимэг

Товч тодорхойлолт

Энэхүү “Open textbook” -ийг бага ангийн багш бэлтгэх их, дээд сургуулийн оюутан, бага ангийн багш нарт зориулав. Тус сурах бичиг нь “Байгалийн ухаан ба бага боловсрол”, “Эх орон ба орчлон ертөнц”, “Байгалийн юмс үзэгдэл”, “Амьд ба амьгүй байгаль “Хавсралт” бүлэг бүрийн төгсгөлд “Асуулт даалгавар” гэсэн бүтэцтэй. Тэрчлэн монголын байгалийн ухааны бага боловсрол, бидний хүрээлэн буй амьд ба амьгүй байгаль, орчныг хоорондын уялдаа холбоонд нь авч үзсэн тул бага насны хүүхдэд байгалийн талаар нэгдмэл ойлголт, төсөөлөл төлөвшүүлэх, өөртөө болон нийгэмд тустай мэдлэг, чадвар, хандлага төлөвшихөд нь туслах ач холбогдолтой юм.

7.3.1.Байгалийн ухаан ба бага боловсрол

Бага боловсролын “Хүн ба байгаль” хичээлийн сургалтын хөтөлбөрийн гол зорилго нь сургалтын хөтөлбөрийн агуулгыг сурагчдад ойлгомжтой, хүртээмжтэй хүргэж, үр дүнтэй хэрэгжүүлэх явдал юм. Ингэхдээ дараах зарчим баримтална:

• Хүүхэд бүрийн авьяас, сонирхол, чадвар, хувийн онцлог шинжийг нээх, дэмжих, хөгжүүлэх үндэс болох;
• Агуулга нь өргөсөх ба гүнзгийрэх залгамж холбоотой, тасралтгүй, сурлагын ахиц дэвшлийг хангахуйц байх;
• Тухайн насны суралцагчдын нас, сэтгэхүй, хөгжлийн онцлогт нийцсэн байх;
• Суралцагчдад сурах арга барил, чадвар эзэмшүүлэхэд чиглэсэн байх;
• Шинжлэх ухааны онолын мэдлэгийг амьдралд хэрэглэх чадвар эзэмшүүлэхэд чиглэсэн байх;
• Хүүхэд бүртэй ажиллах арга зүйд суурилан сургалтын агуулга, аргазүйг уян хатан төлөвлөх, зохион байгуулах нөхцөлийг бүрдүүлсэн байх;
• Эцэг эх олон нийтийн оролцоог хангасан, бие даасан, нээлттэй сургуулийн менежмент, бодлогыг дэмжсэн байх явдал юм.

Судлагдахуун бүрийн агуулгыг сонгохдоо: математик, хүн ба орчин, хүн ба байгаль, англи хэлний хичээлийн агуулгыг олон улсын ерөнхий боловсролын хөтөлбөртэй нийцүүлэн боловсруулсан I-V ангийн математик, англи хэл, байгалийн шинжлэлийн хөтөлбөртэй уялдуулсан байх; төрөлх хэл, “Хүн ба нийгэм” хичээлийн агуулга нь нийгмийн харилцааны бүхий л орчинд эх хэлээрээ чөлөөтэй харилцах, оршин буй нийгмээ танин мэдэх, үндэснийхээ түүх, соёлоор бахархах үзлийг төлөвшүүлэх; урлаг (хөгжим, дүрслэх урлаг, технологи), биеийн тамирын хичээлийн агуулга нь суралцагч гоо сайхныг мэдрэх, түүнийгээ бүтээлчээр илэрхийлэх аргад суралцахад чиглэсэн байхад голлон анхаарвал зохино.

Бага насны хүүхэд бүрийг эх хэл, үндэсний соёл, ёс уламжлалаа эрхэмлэдэг, сурах арга барилтай, авьяас чадвараа нээн хөгжүүлдэг, өөртөө итгэлтэй, бүтээлч сэтгэлгээтэй, эрүүл аж төрөх зөв дадал хэвшилтэй, насан туршдаа суралцах, хамтран ажиллаж амьдрах чадвартай, иргэн болж төлөвшихөд чиглэсэн сургалт, үйл ажиллагааг зохион байгуулна.

Цөм хөтөлбөрийг суралцагчийн чадвар, сурах арга барил эзэмшилт, хувь хүний төлөвшил, тэдний танин мэдэхүйн хөгжлийг гол үзүүлэлт болгон I-III, IV-V анги гэсэн хоёр шатлалтайгаар хэрэгжүүлнэ.

Ерөнхий боловсролын сургууль нь орон нутаг, сургуулийн онцлог, хүний дотоод нөөцийг тооцон цөм хөтөлбөрийг хэрэгжүүлэх арга зүй нь уян хатан, нээлттэй байхаар төлөвлөн сургалтын хөтөлбөр боловсруулан хэрэгжүүлэх боломжтой.

Цөм хөтөлбөрийг хэрэгжүүлэх арга зүй нь дараах шаардлагыг хангасан байна: Хүүхэд өөрөө мэдлэг бүтээх; Тэгш хамран сургах; Суралцагчдын ялгаатай байдлыг харгалзах; Алдаанаасаа суралцахад нь анхаарах; Асуултаар үйл ажиллагаа, суралцагчийн хөгжлийг дэмжих; хүүхэд үйлийн явцад болон тоглох явцад хөгжих, төлөвших.

Бага боловсролын цөм хөтөлбөрийг хэрэгжүүлэхийн тулд суралцагч танхимд болон танхимаас гадуурх байгаль, нийгэм, соёлын ба үйлийн орчин, суралцаж хөгжих нөхцөл боломжийг бүрдүүлэхийг чухалчилна. Сургалтад дүрст ба дуут бичлэг, хэвлэмэл, бодит, цахим хэрэглэгдэхүүн зэргийг ашиглана. Орон нутаг, сургуулийн онцлог, боломжийг харгалзсан, аюулгүй, хямд, ашиглахад хялбар, олдоцтой гарын доорх материалаар сургалтын хэрэглэгдэхүүнийг бэлтгэж болно.

Сургалтын хөтөлбөрийг бүрдүүлж байдаг хүчин зүйлд судлагдахууны суурь ойлголт, сургалтын стандарт, зорилго, сурах бичиг, суралцах хугацаа, багшийн заах арга зүй, ур чадвар багтдаг.

Байгалийн ухаан нь дараах хэдэн онцлогтой: 1-рт уг ухаан нь туршилт, туршлага дээр суурилдаг, 2-рт логик ойлголтод түшиглэдэг, 3-рт шинжлэх ухааны мэдлэг нь аливаа нэг хүний мэдлэг бус олонхоороо хүлээн зөвшөөрөхүйц зүйлийн талаарх ажиглалтад үндэслэсэн мэдлэгийг хэлдэг, 4-рт өдөр тутмын амьдралд болж буй үйл явцад ажиглалт, туршилт явуулж байгалийн үзэгдэлд шинжилгээ хийсний үндсэн дээр зүй тогтол, харилцан хамаарлыг нээн илрүүлдэг, 5-рт Шинжлэх ухааны чухал нээлт нь дараагийн чухал нээлтийг илрүүлэн гаргах эхлэл болдог, 6-рт Шинжлэх ухааны үр дүнгүүд нь хоорондоо харилцан хамааралтай үргэлжилсэн шинж чанартай байдаг.

Байгалийн шинжлэх ухааны мэдлэг нь үнэн баримт, үзэл баримтлал, зарчим, ойлголт, зүй тогтол, хууль, онол, загвар гэсэн бүрдэл хэсэгтэй бөгөөд судалгаа, туршилтын үндсэн дээр бий болж практикаар нотлогдсоны дараа үнэн болдог билээ. Үүнтэй холбоотойгоор шинжлэх ухааныг бүрдүүлдэг мэдлэг нь судалгааны аргатайгаа нягт холбоотой. Иймд их дээд сургуульд суралцаж буй оюутан, тухайлбал бага ангийн багш болох гэж байгаа оюутан байгалийн шинжлэх ухааны судалгааны аргуудыг эзэмшиж, энэ талын тодорхой боловсролтой байхыг цаг үе шаардаж байна.

Үүний зэрэгцээ шинжлэх ухааны мэдлэгийг эзэмших зэвсэг болсон судалгааны арга зүйгээ боловсролын зорилгод нийцүүлэн оновчтой хэрэглэж чадваас үр дүнд хүрч чадна. Ингэж үр дүнд хүрэхийн тулд эрдэмтдийн бүтээл, онол, үзэл баримтлалыг нарийвчлан судалж, туршлагаас нь бүтээлчээр суралцаж, боломжтой бол санал солилцдог. Ил тод мэтгэлцээний үр дүнд хэрэгцээтэй санаа туршлагыг нь авч, боломжгүйг нь авах гээхийн ухаанаар шүүж, практикт хэрэглэх нь ихэд дэлгэрчээ. Зарим оронд явуулсан судалгаанаас үзвэл олж авсан мэдлэгийг түгээхээс илүү байгаль судлал руу түлхүү анхаарах болсноор шинжлэх ухааныг судалгааг илүүд үздэг болсон байна.

Товчоор судалгаа бол шинжлэх ухааны мэдлэгээс бүрдсэн, өмнө хуримтлуулсан мэдлэг, шинжлэх ухааны үйл явц, шинж чанарыг ашиглан шинэ мэдлэг бүтээх цогц үйл ажиллагаа юм. Шинжлэх ухааны судалгаанд ажиглалт, туршилт гэх мэт бодит үйл ажиллагаанаас гадна шинжлэх ухааны мэдлэгт түшиглэн шинээр үүсэн бий болсон шинжлэх ухааны холбогдолтой асуудлыг шийдэх үйл ажиллагаа ч багтдаг.

Бодит үзэгдэлд суурилсан ажиглалт, туршилт явуулж материал бүрдүүлснээр ерөнхий дүгнэлтийг гаргаж авах индукцийн арга, мэдлэг, туршлагадаа үндэслэн шинээр үүсэн гарч ирсэн асуудлыг шийдвэрлэхийн тулд таамаглал дэвшүүлэн туршилт судалгаа хийх, дэвшүүлсэн таамаглалаа батлах, ингэснээр шинэ мэдлэгийг бүтээх дедукцийн арга байдаг.

Одоо байгалийн шинжлэх ухааны судалгааны үйл явц, судлаачийн ур чадвар ямар холбоотойг авч үзье. Судалгааны аргууд олон ч эдгээрээс нийтлэг аргууд байдаг бөгөөд судалгааны үр дүнгийн бодит байдал нь үйл явцын оновчтой төлөвлөлт, шийдэл, судлаачийн ур чадвараас хамаарах тал бий.

Өнгөрсөн зууны жараад онд АНУ-ын байгалийн ухааныг хөгжүүлэх нийгэмлэг (AAAS)-ээс боловсруулсан судалгаанд суурилсан бага боловсролын байгалийн ухааны сургалтын хөтөлбөр болох SAPA(Science-A Process Approach)-ыг хэрэгжүүлсэн бөгөөд үүнд судалгааны ур чадварыг үндсэн ба интеграцчилсан ур чадвар хэмээн ангилж авч үзсэн байна. Үүнээс хойш олон судлаач энэхүү хөтөлбөрийг баяжуулж, бас хасаж хэрэглэсээр иржээ. Ерөнхийдөө суурь хөтөлбөрийг бага ангид, харин цогц хөтөлбөрийг дунд ангид сонгон заах нь тохиромжтой. Гэхдээ ангиас үл хамааран багш судлах сэдэв, нөхцөлөөсөө хамааруулан бага ангид цогц хөтөлбөрөөр орох боломжтой бөгөөд дунд ангид ч суурь хөтөлбөрөөр судалгааны хичээл оруулж болно. Ингэж судалгааны хичээлийг орохдоо зөвхөн ганц аргыг сонгох бус, харин судалгааны тохирох аргуудыг хослон хэрэглэх нь элбэг.

Одоо АНУ-ын 2007 онд байгалийн ухааны сургалтын хөтөлбөрт туссан багшийн судалгааны ур чадварын агуулгатай танилцъя. Бага боловсролын багш хэн боловч хүрээлэн буй байгаль орчныхоо талаар тодорхой хэмжээний мэдлэгтэй байхын зэрэгцээ бага насны хүүхдүүдийг судлах судалгааны аргуудыг эзэмшсэн байх шаардлагатай байдаг. Тэр дотроо бага насны хүүхдүүдийг танин мэдэх үйл явц, сэтгэхүйн болон бие бялдрын хөгжлийн явцыг байнга ажиглан судалсны үндсэн дээр тэдэнтэй ажиллах арга зүйгээ оновчтой сонгодог билээ. Үүнтэй холбоотойгоор бид суурь судалгаа гэж юу болох, түүнийг хэрхэн гүйцэтгэх, үр дүнгээ яаж нэгтгэж дүгнэх асуудлыг дараах хэсгээр авч үзлээ.

1. Ажиглалт: Ажиглалт нь бүх үл мэдрэх болон мэдрэхүйг хөгжүүлж өгдөг багаж хэрэгсэл (микроскоп, томруулагч дуран г.м) ашиглан юмс үзэгдэлтэй холбоотой хэрэгтэй мэдээлэл, материалуудыг цуглуулах үе шат юм.
2. Ангилал: нь тодорхой нэг зорилгоор аливаа юмсын нийтлэг тал ба ялгаатай талуудыг ангилан авч үздэг. Өөрөөр хэлбэл, арга, тогтолцоогоор нь ангилан хуваахыг хэлнэ. Ангиллыг аливаа юмс, үйл хөдлөлийн нэгдлийг эмх цэгцтэй болгоход ашигладаг. Эд юмс, үйл хөдлөлийн ижил ба ялгаатай тал, харилцан хамаарал зэргийг харуулахын тулд ангилах аргыг ашигладаг. Жишээ нь: Холимог зүйлсийг өнгө, хэлбэр, шинж чанараар нь ангилах’, ’ олон төрлийн чулууг хэмжээ, өнгө, хатуулаг чанараар нь ангилах гэх мэт.
3. Хэмжилт: Шинжлэх ухааны үүднээс асуудлыг шийдвэрлэх явцад таван мэдрэхүйг ашиглан мэдээлэл цуглуулахаас гадна тогтсон хэм хэмжээний мэдээллийг цуглуулах арга байдаг бөгөөд үүнийг хэмжилт гэдэг. Өөрөөр хэлбэл, хэмжилт нь ажигласан зүйлээ хэмжих үйл явц бөгөөд урт, хүндийн жин, эзлэхүүн гэх мэт хэмжээг хэмжиж тэмдэглэх арга юм. Жишээ нь: 50м гүйхэд зарцуулах цагийг секунд хэмжигчээр хэмжих, усны халах хэмжээг термометрээр хэмжих
4. Таамаглал нь ажиглалт, хэмжилтэд үндэслэн тогтвортой байдлыг нь тооцоолж дараа нь гарч болох нөхцөл байдлыг урьдчилан тооцоолж таамаг дэвшүүлэхийг хэлдэг. Ажиглалт, үндэслэлтэй материал дээр суурилсан таамаглал биш бол түүнийг шу-ы үндэслэлтэй таамаглал гэж үзэхгүй. Зөв таамаглал нь нарийн ажиглалт, тодорхой хэмжилт, өөрчлөлт явагдах болсон учир шалтгаан зэрэгт үндэслэдэг. Жишээ нь: Шилэн лонхонд байгаа лааны унтрах цагийг хэмжсэний дараа үүнээс 2 дахин том шилэн лонхон дахь лаа хэзээ унтрахыг урьдчилан таамаглах, туухайг зөөхөд хэвтээ байдлаас хэрхэн зөөх талаар таамаглах.
5. Судалгааны дүгнэлт нь ажиглалтыг тайлбарлах явц. Ажиглалт нь мэдрэхүйг ашиглан тухайн зүйл, нөхцөл байдлын талаарх материал байдаг бол дүгнэлт нь ажиглалтын явцад үүссэн учир шалтгааныг тайлбарлах, олох явдал юм. Жишээ нь: Усанд мөс хийхэд мөс хайлдаг учир шалтгааныг дүгнэх, өвс болон навчин дээр шүүдэр тогтдог учир шалтгааныг дүгнэх
6. Холбоо хамаарал нь өөрийн санаа бодлыг бусадтай хуваалцан, бусдын санаа бодол мэдээллийг ойлгох явдлыг хэлдэг. Холбоо хамаарлын аргад үг хэлээр ойлголцохоос гадна бичгээр, биеийн хэлээр, зургаар, графикаар ойлголцох аргууд байдаг. Судалгааны тайлан бичих, бусдыг судалгааг унших нь мөн адил холбоо хамаарлын бас нэг арга юм. Холбоо хамаарлын судалгааны явц ур чадварт багтаан авч үзэхгүй байх нь олонтоо. Учир нь хэлний харилцаа холбооны ойлголттой давхарддаг гэж үздэгтэй холбоотой. Гэвч шинжлэх ухааны туршилтад нийгмийн талын бүрэлдэхүүн хэсэг чухал байр суурьтай байдаг гэдэг үүднээсээ судалгааны үр дүнг холбоо хамаарлаар илэрхийлэх нь маш чухал.
7. Шийдвэрлэх асуудлыг олж харах. Шийдвэрлэх асуудлыг олж харан мэдлэг дээрээ суурилан асуудлыг дахин боловсруулах явц юм. Жишээ нь: Электрометрт нөлөөлдөг хүчин зүйлс? Ургамлын навч болон үндэсний хэлбэр нь ямар хамааралтай вэ?
8. Таамаглал дэвшүүлэх: Ойлголт, ажиглалтад үндэслэн гаргалгаа гаргасны дараа зөв гэж бодсон зүйлийнхээ тухай батлах үйл явц. Таамаг дэвшүүлэх нь төлөвлөсөн туршилт, судалгаа явуулахад чухал үүрэгтэй бөгөөд хязгаарлагдмал, хэлбэр төдий байдаг. Таамаглал дэвшүүлэх нь мэдээлэл ашиглан туршилтын үр дүнгийн талаар урьдчилан таамаглах явц. Урьдчилан таамаглах ойлголт нь туршлагад суурилдаг бол таамаглал дэвшүүлэх ойлголт нь бүхэлд нь хамрах шинжтэй байдаг. Жишээлбэл: Лааны дээрээс аяга тавихад лаа унтарна гэдэг нь урьдчилсан таамаг бол хүчилтөрөгч шатсанаас болж лаа унтарна гэдэг ойлголт нь таамаглал дэвшүүлэх ойлголт юм. Жишээ: Дамжуулагч утасны ороолтын тоо ихсэх тусам электометрийн чадал нь нэмэгддэг, халах тусам хийн төлөвийн эзлэхүүн нь ихэсдэг.
9. Хувьсах хяналт. Хувьсах хяналт нь туршилт хийх зорилгоор өөрчлөх ёстой хувьсагч мөн туршилтад нөлөөлж болохуйц хувьсагчийг нийтэд нь хянах үүрэгтэй. Учир шалтгааны холбоог тайлбарлахын тулд хувьсагч нь бие даасан хувьсагч, үүний нөлөөгөөр үүссэн хувьсагчийг хамааралтай хувьсагч гэдэг. Хувьсах хянагч нь туршилтын үр дүнд нөлөөлж болох хувьсах хэмжигдэхүүнүүдийг тодорхойлж, бие даасан хувьсагчийг өөрчлөх явцад бусад хувьсагчид тогтмол байхыг хэлнэ. Энэ үед тогтмол, хяналттай байдаг хувьсагчуудыг ‘хяналтын хувьсагч’ гэдэг. Шинжлэх ухааны судалгаагаар системчилсэн байдлаар нэг хувьсагчийг өөрчлөхийн зэрэгцээ үлдсэн хувьсагчуудыг нарийн хянаж хувьсагч хоорондын хамаарлыг тодорхойлох боломжтой. Жишээ: цахилгааны хүчин чадал, хадаасны хэмжээ гэх мэтийн хувьсагчийг хязгаарлах, төмөр утасны ороолсны тоогоор цахилгаан соронзын хүчдэлийг харьцуулна. Ургамалын төрөл, хэмжээ, хүрээлэн буй орчин гэх мэтийн хувьсагчийг хянаж, навчны тоогоор өсөлтийн нөлөөг харьцуулна.
10. Өгөгдлийн хувиргалт: Ажиглалт, хэмжилтийн үр дүнгээс олж авсан өгөгдлийг бүртгэх, өгөгдлийг ойлгомжтой хялбар байлгах үүднээс хүснэгт, график болгон хувиргах явцыг хэлдэг. Өгөгдөл хувиргах замаар их хэмжээний мэдээллийг танихад хялбар бөгөөд өгөгдлийн чиг хандлага болон тогтмол шинжийг хялбархан олох боломжтой. Жишээ: 1 жилийн турш сар бүрийн хур тунадасны хэмжээг графикаар харуулах, ус халааж тодорхой хугацаанд шугаман графикаар харуулах.
11. Өгөгдлийн тайлбар нь цуглуулсан өгөгдлийг ажиглалт, туршилт, судалгаагаар шинжлэх, өгөгдөлд буй утгыг ойлгох, тайлбарлахад оршино. Өгөгдлийг тайлбарлахын тулд түүнийг зохих хүснэгт, график, диаграмм болгон өөрчлөх шаардлагатай бөгөөд өгөгдлийн өөрчлөх үйл явц нь өгөгдлийн тайлбар хэсэгт хамаардаг. Жишээ: Лабораторийн шилэн аяганы хэмжээ нь лаа унтарсан хугацаанд пропорциональ, усыг тасралтгүй халаавал температур нь өсөж байгаад тодорхой температурт хүрээд тогтмол болдог.
12. Дүгнэлт. Тайлбарласан өгөгдөлд үндэслэн асуудлын хариуг олж авах болон таамаглалын талаарх шийдвэр гаргах явц юм. Дүгнэлт нь судалгаа шинжилгээний хураангуй биш боловч судалгааны сэдэв, таамаглалын талаарх баттай таамаглал юм. Өгөгдлийн тайлбарлах нь тухайн өгөгдлийг тодорхойлох үйл явц юм. Дүгнэлт нь өгөгдлийн утгыг тодорхойлох үйл явц юм. Жишээ нь: Нарны гэрлийн хэмжээ нь ургамлын өсөлтөд нөлөөлдөг, төмөр утаснуудын ороодосны тоо нь цахилгаан соронзон орны хүчдэлд нөлөөлдөг.
13. Түгээмэл байдал: Тодорхой жишээ, батлагдсан баримтаас гаргаж авах үйл явц юм. Түгээмэл байдал нь нэгэн бүхэл цогц дүгнэлт юм. Ялангуяа хувьсагч хоорондын холбоо хамаарлын түгээмэл байдлыг хууль, зүй тогтол гэдэг. Өгөгдлийн тайлбар ба дүгнэлт нь аливаа нэг үйл явц болон өгөгдлийг илэрхийлдэг бол түгээмэл байдал нь олон төрлийн өгөгдөлд суурилсан иж бүрэн утгыг бий болгодог. Жишээ нь: Биет нь халбал тэлдэг, бодисууд нь үндсэн 3 төлөвт оршдог.
14. Шинжлэх ухаанд хандах хандлага нь шинжлэх ухааныг судлах, сурахад маш чухал хөдөлгөгч хүч болдог. Шинжлэх ухааны хандлагыг шинжлэх ухаанч хандлага, шинжлэх ухааны тухай хандлага гэсэн 2 хэсэгт хуваан авч үздэг. Шинжлэх ухааны тухай хандлага нь шинжлэх ухаан, салбар ухааны талаарх сонирхлын хэм хэмжээг илэрхийлдэг. Суралцагч шинжлэх ухаанд эерэг ханддаг бол шинжлэх ухааны үзэгдэл, үйл ажиллагааг нааштай тусган авч идэвхтэй оролцдог. Шинжлэх ухаанд сонирхолтой оюутнууд нь илүү нээлттэй хандаж асуудалтай тулгарвал нөхцөл байдлыг эергээр хүлээн авч шийдвэрлэх аргыг идэвхтэй эрэлхийлэх хандлагатай болдог. Нөгөө талаар, шинжлэх ухааны хандлага нь шинжлэх ухааныг зөв хэрэгжүүлэх арга, хандлагыг хэлдэг. Эрдэмтэд шинжлэх ухааны хандлагын тухай олон янзаар тайлбарлан авч үзсэн байдгаас заримаас нь авч үзье.
15. Сониуч зан. Эрдэмтэд байгаль ертөнцийг ойлгохын тулд сониуч зандаа хөтлөгдөн судалгаагаа хийж эхэлдэг. Өөрийнхөө эргэн тойрны үзэгдлийг ажиглан тэндээс ямар нэг асуудлыг хайн олж, түүний хариултыг олох гэж эрмэлзэх тэр хандлага нь шу-ны хөгжилд маш чухал үүрэг гүйцэтгэдэг. Сурагч зохих ёсоор сурах эрмэлзэлтэй бол байнга сонирхож, мэдэхийг эрмэлзэн эрэл хайгуул хийдэг болох нь гарцаагүй.
16. Нээлттэй байдал. Байгаль ертөнцөд тодорхой бус зүйлс оршин байсаар ирсэн. Энэ тухай шинжлэх ухааны түүхээс хялбархан харж болно. Нэгэн үе жинхэнэ үнэн хэмээн үзэж байсан Птолемейн онол нь Коперникийн онол болж өөрчлөгдсөн бол хэзээ ч хувирахгүй мэт итгэж байсан механик хөдөлгөөний тухай Ньютоны хууль нь Эйнштейний харьцангуй онол гарч ирснээр хязгаарлагдмал байдалд орсон байна. Энэ мэт явдлаас харвал шинжлэх ухаанч хүн өөрийн дүгнэлт, бусдын дүгнэлтийг нээлттэй, шүүмжлэлтэй талаас харах ёстой. Нотолгоо баримтад үндэслэн аливаа юмс, үзэгдлийн тухай авч үзэхэд өөр тайлбар шаардлагатай гэж үзсэн тохиолдолд өөрийн тайлбартаа өөрчлөлт хийж чаддаг байх ёстой. Сурагчид ч мөн адил өөрийнхөө шинээр илрүүлсэн үндэслэлийн талаарх дээрх өөрийн санаа бодол, байр сууриа өөрчлөх чадвартай байх ёстой ажээ.
17. Бодит шинж. Шинжлэх ухааны үйл ажиллагаа явуулахдаа аливаа нэг хүний хувийн үзэл бодолд автах ёсгүй бөгөөд бусдын үзэл бодол, шахалтад автаж болохгүй. Байгалийн үзэгдлийн ажиглалт, тэдгээрийн тайлбар нь хувь хүний өөрийнх нь туршлага, үзлээс хамааралтай байдаг. Гэсэн хэдий ч, өөртөө болон бусад хүмүүсийн санаа бодол, байр сууринд үл автан өгөгдлийг аль болох бодитойгоор харж, тайлбарладаг байх хэрэгтэй.
18. Шийдвэрээ дахин нягтлах. Шинжлэх ухааны судалгаа шинжилгээг явуулахдаа хангалттай бус нотолгоонд үндэслэн дүгнэлт гаргах явдлаас зайлсхийж гаргасан дүгнэлт нь зөв эсэхийг дээр анхаарч үзэх шаардлагатай. Нотолгоо материал хангалтгүй бол нь буруу үр дүн, дүгнэлтийг хийхэд хүргэнэ. Тиймээс амжилттай сайн үр дүнд хүрэхийн тулд илүү олон баттай их өгөгдөл, нотолгоо олтлоо хүлээж тодорхой бус нөхцөл байдлыг хүлээн зөвшөөрөх ёстой. Түүнчлэн өөр үздэг үзэл бодлыг хүндэтгэх хэрэгтэй.
19. Баримт нотолгоонд суурилах. Шинжлэх ухаанч үзэл нь бусад үзлээс ялгардаг шинж чанар бол нотлох баримтад тулгуурласан байдагт оршино. Энэ нь шу-ы салбар бусад салбартай харьцуулбал эрх мэдэл гэх зүйлгүй, субьектив үзэлд суурилсан шийдвэр, үр дүнгээс хараат бус бага хамааралтай байдаг гэсэн үг юм. Шинжлэх ухаан нь нотолгоонд тулгуурладаг. Тиймээс суралцагчдын хувьд шинжлэх ухааны судалгаа хийхдээ шинжлэх ухааны үндэслэлтэй тайлбар, нотолгоог батлахуйц өгөгдлийн олж, цуглуулах, үр дүнг гаргахдаа ч баримтад тулгуурладаг байх нь маш чухал.
20. Үнэнч шударга байдал. Эрдэмтэд эрдэм шинжилгээний бүтээлээ албан ёсоор хэвлэн нийтэлж, илтгэл тавьдаг бөгөөд бусад хүмүүс эдгээр илтгэлүүд дээр үндэслэн туршилт, судалгааны ажлаа хийдэг. Гэвч эрдэмтэд туршилтын үр дүнг гажуудуулж буруу илтгэл тавьсан тохиолдолд шинжлэх ухааны салбарын судалгааны ажил ёс суртахууны хувьд ч маш сөрөг үр дагавар авчирдаг. Суралцагчид ч мөн адил шинжлэх ухааныг судлахдаа шударга байхыг эрмэлзэх ёстой. Суралцагчид ажигласан зүйлсээ үнэн шударгаар тайлагнадаг байх ёстой. Өгөгдөл, үр дүнг ямар нэг зорилгоор гуйвуулж болохгүй. Тэд үзэл бодлоо зөв, эсвэл буруу байхаас үл хамааран санаагаа шударгаар илэрхийлэх чадвартай байх ёстой. Ингэхийн тулд суралцагчид хичээл дээрээ судалгаа шинжилгээнийхээ үр дүнгийн тухай чөлөөтэй илэрхийлэх орчныг бүрдүүлэх нь чухал.
21. Шүүмжлэлтэй хандах. Шүүмжлэл гэж нь аливаа нэг үнэн, үзэл баримтлалыг шууд хүлээж авалгүй зөв буруу эсэхийг нь нягталж үзэн шүүмжлэлтэй ханах хандахыг. Шинжлэх ухааны онолууд, бусад хүмүүсийн санал бодол, өөрийнхөө үзэл бодлыг ч мөн зөв эсэхийг нягталж үздэг байх нь чухал. Шүүмжлэл байхгүй бол бусдын үзэл бодлыг сохроор дагах, үндэслэлгүй шийдвэр гаргахад хүргэнэ.
22. Хамтарсан судалгаа. Шинжлэх ухааны судалгааг ганцаараа гүйцэтгэх нь ховор байдаг бөгөөд хэд хэдэн хүмүүс баг болж хамтран ажиллах нь элбэг. Дэлхийд нэртэй шинжлэх ухааны сэтгүүлээс харсан ч, нэг эрдэмтний хийсэн судалгаа ховор байдаг бөгөөд ихэнхдээ хамтарсан судалгаа шинжилгээ байдаг. Тиймээс хамтын ажиллагаа нь шинжлэх ухааны үйл ажиллагаа явуулахад маш чухал. Хамтран судалгаа хийснээр илүү сайн судалгааны үр дүнд хүрч чадна. Бусадтай хамтарч чадахгүй бол шинжлэх ухааны хүрээнд орж чадахгүй. Сургуулийн шинжлэх ухааны хичээл ч үүнтэй адил.
23. Бүтэлгүйтсэн ч эергээр тусгаж авах. Алдаа нь тодорхой бус зүйлийг судлахад хэн бүхний туулаад гардаг даваа юм. Эрдэмтэд бүтэлгүйтлийг эергээр хүлээн авч, эдгээр алдаа дутагдлыг илүү сайн хөгжих суурь болгон ашигладаг. Алдаа нь эцсийн цэг бус харин ч шинээр эхлэх цэг юм. Түүхээс харахад бүтэлгүйтлээс үүдэн амжилтад хүрсэн олон жишээ бий. Байгалийн шинжлэх ухааны хичээл дээр суралцагчдын хийж буй судалгааны ажил нь бүтэлгүйтэж алдаа гаргаж болно гэдгийг мэддэг байх хэрэгтэй. Алдаануудыг сөргөөр хүлээн авах бус алдаагаа засаж дахин шинээр судалгаагаа хийж, асуудлыг шийдвэрлэхийн төлөө хичээллэн зүтгэж ажиллах хэрэгтэй.

7.3.2. Эх орон ба орчлон ертөнц

Хоорондоо холбоо бүхий одод, оддын бөөгнөрөл, тэдгээрийн хоорондох орчныг нийтэд нь галактик буюу оддын аймаг гэж нэрлэнэ. Оддын аймгийн одод, гараг, тоосонцруудыг хамтад нь орчлон ертөнц гэнэ. Одот ертөнц нь тус бүрдээ хэдэн зуун тэрбум одыг багтаасан хэдэн зуун тэрбум галактикаас бүрдэх хязгааргүй уудам орон зай юм.

Зураг II.1. Одот ертөнц

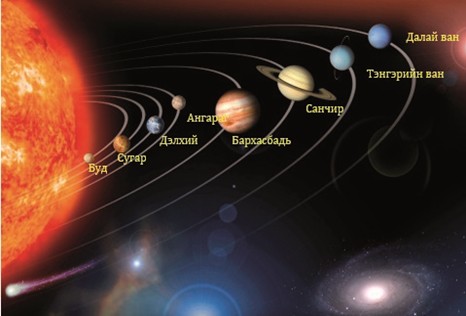
Зураг II.2. Нарны аймаг

НАР, САРНЫ ХӨДӨЛГӨӨН

Нар бол бидэнд хамгийн ойр орших шар од юм. Нар бол асар том хэмжээний халуун улайссан хийнээс тогтсон бөмбөрцөг хэлбэртэй эрхэс юм. Түүний диаметр нь 1 392 мянган км, дэлхийн диаметрээс 109 дахин том, эзлэхүүн нь 1,3 сая дахин их. Нарны масс нь дэлхийнхээс 333400 дахин их. Жингийн хувьд нарны аймгийн бүх гарагийн цулаас 745 дахин их, татах хүчний хурдатгал дэлхийнхээс 28 дахин их байгаа нь манай эндхийн 1 кг жинтэй биет нь тэнд 28 кг болно гэсэн үг. Нар дэлхийгээс 150 сая км зайд оршдог.

Зураг 26. Нар

Сар. Гарагуудын ихэнхийг дагуул нь тойрон эргэдэг. Буд, Сугараас бусад нь дагуултай. Нийт 60-аад дагуул одоогоор мэдэгдээд байна. Эдгээрээс хамгийн том нь болох Санчир гарагийн дагуул Титан нь Буд гарагаас арай том. Манай дэлхийн цорын ганц дагуул болох дэлхийгээс 384400 км зайтай оршдог Сарны диаметр 3475 км. Бидэнд хамгийн ойр орших тэнгэрийн эрхэс-сар илүү сайн судлагджээ. Нягт нь 3,34 г/см3, саран дээр хүндийн хүч дэлхийнхээс 6 дахин бага. Агаар мандал, усны уур байхгүй учир цаг агаарын янз бүрийн үзэгдлүүд байхгүй, дуу авиа дамжихгүй, нарны цацраг ойж сарнихгүй болохоор тэнгэрийн өнгө нь хар харагддаг. Сарны гадаргын температур өдрийн талдаа +123°С, шөнө болж буй талдаа – 153°С хүрдэг. Учир нь сар тэнхлэгээ удаан эргэдгээс гадна агаар мандал байхгүйтэй холбоотой.

АСУУЛТ ДААЛГАВАР

• Жижиг гарагуудын хэлбэр ба орбит нь том гарагуудынхаас ямар ялгаатай вэ?
• Дэлхийд хамгийн ойр орших хоёр гарагийг нэрлэж, дэлхийтэй харьцуулж ярилцана уу.
• Саран дээр өдөр шөнө тус бүр хэдэн хоног үргэлжлэх вэ?
• Сүүлт одны сүүл үүсэх шалтгааныг тайлбарла.
• Өөрийн төрсөн одны ордыг нэрлэ. Энэ нь ямар учиртай вэ?
• Яагаад нар, сарны хиртэлт болдгийг зургаар тайлбарлана уу.
• Нар од юм бол нар бар харвах уу? Од харвах үзэгдлийг тайлбарлана уу.
• Манай оронд солир унаж байсан мэдээ бий юу.
• Яагаад монголчууд од харвах үед миний од биш тэнгэрийн од гэж хэлдгийн утга учрыг тайлбарлана уу.

7.3.3. БАЙГАЛИЙН ЮМС ҮЗЭГДЭЛ

Биднийг хүрээлэн байгаа материаллаг биетийг бүрдүүлж байгаа юмсыг бодис гэнэ. Бодис бүхэн молекулуудаас тогтоно. Молекул бүхэн атомуудаас тогтоно. Атом гэдэг үг нь грек хэлний “хуваагдашгүй” гэсэн утгатай. 2400 жилийн өмнө эртний Грекүүд ертөнцийн бүх биет атомоос бүрддэг гэж бичиж үлдээжээ.

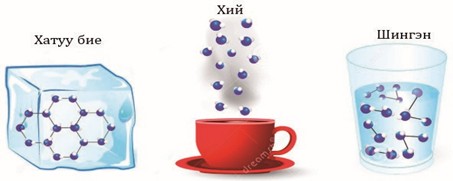
Зураг 27. Бодисын төлөв

7.3.4. АМЬД БА АМЬГҮЙ БАЙГАЛЬ

Бүх дэлхийн амьд организм амьдардаг дэлхийн бүрхэвчийг биомандал буюу шим мандал гэнэ. Дэлхий дээр амьдралын анхны хэлбэр 3 тэрбум гаруй жилийн өмнө үүссэн байна. Биомандал гэдэг нэрийг анх 1875 онд австрийн геологич Э.Зюсс хэрэглэжээ. Биомандал нь амьд организмын амьдралын процесс явагдаж байдаг онцгой хүрээ юм. Анхны нэг эст амьтан 2,7 тэрбум жилийн өмнө, олон эст амьтан 1-1,5 тэрбум жилийн өмнө үүсжээ. Амьд бодисын нийт тоо хэмжээг биомасс гэнэ. Биомассыг кг/м2, кг/м3, т/га зэрэг нэгжээр илэрхийлдэг. Одоо манай гараг дээр 500 мянга гаруй зүйлийн дээд ургамал, 1,5 сая зүйлийн амьтан, 7 тэрбум хүн амьдарч байна. Амьд биеийн биомасс нь чулуун мандлын массын дөнгөж 0,01%-ийг эзэлдэг. Биомассын ихэнх нь хуурай газарт орших ба далайн биомассаас 200 дахин их юм. Хуурай газарт ургамлын масс нь амьтныхаасаа 1000 дахин их бол, далайд амьтны масс нь ургамлынхаасаа 26 дахин илүү байна.

Зураг 28. Дэлхийн мандлууд

Ургамлыг модлог, сөөг, өвслөг гэж 3 ангилж үзээд тус бүрийг мөнх ногоон - мөнх ногоон биш, цэцэглэдэг - цэцэглэдэггүй, зэрлэг - таримал, дээд – доод гэх мэтээр цааш нь ангилж болно. Үүнээс доод ургамлыг бактери, замаг, салстан, мөөг, хаг, шилбүүртэн;, дээд ургамлыг хөвд хэлбэртэн, шивэрсэн, шаантаг навчтан, ойм хэлбэртэн, нүцгэн үртэн, бүрхүүл үртэн гэж ангилна. Ургамал ихээр тархсан нутгийг ургамлын дэлгэц нутаг гэнэ.

Зураг 29. Ургамал

Ашигласан ном зүй:

1. Дауренбек Ш., Конг Ён Тай (2017) Бага боловсролын байгалийн ухааны үндэс
2. Дауренбек Ш., Кун Ён Тэ, Баярчимэг Б., Хун Ён Ги, Дэлгэрсайхан Ц., И Гён Вон, И Ён Ман (2018) Хүн байгаль хичээлийн агуулга, арга зүй, үнэлгээ
3. Дауренбек Ш., Баярчимэг Б., Кун Ён Тэ, Ли Ён Ман, Дэлгэрсайхан Ц., Канг Хонг Жэй, Энхцэцэг Д., Хадбаатар Б. (2020) Шинжлэн судлах туршилтууд: Хүн ба байгаль
4. Баярчимэг Б., Кун Ён Ги (2017) Бага боловсролын байгалийн ухааны сургалтын агуулга, арга зүй
5. Баярчимэг Б., Нэргүй Г., Дауренбек Ш. (2013), Хүн ба байгаль хичээлийн хялбар туршилтууд
6. Содов, Ц., Батхуяг, С., Баярчимэг Б., Дауренбек Ш., Сансартуяа Х., Уранчимэг Ц. (2017), Байгалийн ухаанд сургах зүй (Сургуулийн өмнөх ба бага боловсролын багш, оюутанд)
7. Батчулуун Е. (2009) Дэлхий судлал
8. Батчулуун Е. (2017) Газарзүйн боловсролын үндэс

7.4. БАЙГАЛЬ ШИНЖЛЭЛ, АРГА ЗҮЙ

С.Батхуяг

7.4.1.УДИРТГАЛ

Орчин цагийн бага насны хүүхдийн, тэр дотроо монгол хүүхдийн өссөн орчин, танин мэдэх сэтгэлгээний онцлогийг мэдэхгүйгээр тэдэнд хүрээлэн буй байгаль орчны талаар ойлголт төлөвшүүлэх боломжгүй. Үүнтэй холбоотойгоор бусад шинжлэх ухаануудын судалгааны арга, сургах аргазүйтэй сайтар холбож, үүнийгээ бүтээлчээр боловсруулж, хичээл үр дүнтэй болно. Судлаачид байгаль шинжлэл арга зүй хичээлийг дараах байдлаар авч үзсэн байна. Тухайлбал:

Их Британийн Лондонгийн их сургуулийн эрдэмтэн Аманда МакКрори, Кенна Уортингтон нар (2017) “орчин үеийн бага боловсролын байгалийн ухааны хичээл нь хүүхэд бүрийг шинжлэх ухааны эрэл хайгуул хийх чадвар, өөртөө итгэх итгэл, шинжлэх ухаанд эергээр хандах хандлага төлөвшүүлэхийн зэрэгцээ шинжлэх ухааны мэдлэг эзэмшин суралцахад нь дэмжлэг үзүүлэх явдал юм” хэмээн үзсэн бол Ц. Содов, С.Батхуяг нар (2017) “байгалийн тухай шинжлэх ухааны суралцагчдад сургах сурган хүмүүжүүлэх процессын зүй тогтлыг судалдаг байгаль шинжлэл арга зүй судлагдахууны зорилго нь байгалийн шинжлэх ухааны баримт, зүй тогтлын тухай энгийн ойлголтуудыг суралцагчдад, судалгааны анхан шатны дадал төлөвшүүлэхэд орших ажээ. Энэ нь сурган хүмүүжүүлэх зүйн ерөнхий ба өвөрмөц зарчмууд байгалийн ухаанд сургахзүйн шинж чанараар тодорхойлогдоно” гэж үзсэн байна. Харин Орос холбооны улсын эрдэмтэн С.В.Блинова (2014) Бага боловсролын байгалийн ухааныг заах арга зүй нь сургуулийн сургалтын хөтөлбөрийн онцлогоор тодорхойлогддог сурагчдын суралцах үйл явц, хөгжлийн тогтолцооны шинжлэх ухаан юм.

Энэ хичээл нь бага ангид хүн ба орчин, хүн ба байгаль хичээлийг зохион байгуулах, бага насны сурагчдад сониуч зан, шүүмжлэлтэй сэтгэх, шинжлэн судлах чадварыг төлөвшүүлж, тэдэнд байгалийн ертөнцийн талаарх суурь ойлголтыг өгөх зорилготой. Энэ нь практик хайгуул, ажиглалт, туршилтад анхаарлаа хандуулж, сурагчдыг асуулт асуух, таамаглал дэвшүүлэх, үйл ажиллагаа төлөвлөх, үр дүнд үндэслэн дүгнэлт гаргахад чиглүүлдэг. Бага боловсролын байгалийн ухааны хичээл нь дунд болон ахлах ангид шинжлэх ухааны илүү ахисан түвшний суралцах суурийг тавьж өгдөг.

7.4.2.БАГА БОЛОВСРОЛЫН БАЙГАЛИЙН УХААНЫ СУРГАЛТЫН ХӨГЖЛИЙН ТОЙМ, ОРЧИН ҮЕИЙН ЧИГ ХАНДЛАГА

Суралцахуйн зорилт:

• Бага анги болон бага ангийн багш бэлтгэх сургалтад судалж ирсэн байгалийн ухааны хичээл, түүний агуулга тэдгээрийн хөгжлийн тоймыг судлах, орчин үеийн чиг хандлагыг судлах

Монголын боловсролын түүхэн үечлэл

• Монголд гэгээрэл боловсролын ажил үүсэж хөгжсөн нь /нэн эртнээс 1920 он/ I-IV үе
  • Эртний Монголын хүмүүжил, гэгээрэл боловсролын ажил /нэн эртнээс XII зуун хүртэл/
  • Монголын эзэнт улсын ба түүний дараах үеийн боловсролын ажил /XIII-XVII/
  • Манжийн дарангуйллын үеийн сургууль /1770-1911 он/
  • Олноо өргөгдсөн Монгол улсын сургууль /1911-1921 он/
• Орчин үеийн Монголын гэгээрэл боловсролын ажил /1921 оноос/ V-VIII үе
  • Бүх нийтийг бүрэн бус дунд боловсролтой болгох зорилтыг хэрэгжүүлсэн нь /1958-1985 он/ VII үе
  • Улс орны өөрчлөн байгуулалт, ардчилсан шинэчлэлтийн үеийн боловсролын ажил /1987-2009.10 сар хүртэл/ VIII үе

Монгол улсын дотоод Яамны шийдвэрээр 1922 оны намрын сүүл сард Нийслэл хүрээнд Багш бэлтгэх түр курсийг Б.Ишдорж, Баатар нарын багштай эхэлжээ.

Сурах бичиг:

• Байгалийн шинжлэл. Тэргүүн дэвтэр. Хий, ус, шороо гурван мах бодын зүйл. 1929 он. Улаанбаатар

Багшийн сургуулийн байгалийн ухааны хичээлийн түүхэн тойм

Он	Хичээлийн нэр	Багшийн нэр
1922	Хүний биеийн анатоми, Лунчивичла “Байгаль бодисын анхлан судлах бичиг” орчуулга, И.Трудновский “Байгаль шинжлэлийн сурах бичиг” орчуулга	Б.Ишдорж
1923	Дэлхийн байдал, Түмэн бодис	Батхаан
1927	Дэлхийн байдал, Түмэн бодис, Орон нутгийн байдал	Б.Ишдорж
1928	Түмэн бодис, Дэлхийн байдал, Монгол орны нутгийн байдал, төрх, дүрс	Ц.Жамсранов Цэвэгжав-Дашеев, Эрдэнэсайхан
1929	Түмэн бодис /9ц/, Дэлхийн байдал /6ц/, Монголын орон нутгийн байдал ба аж ахуй /8ц/	Ванчиг, Балжид, Ц.Жамсранов
1930	Дэлхийн байдал, хүний биеийн анатоми, түмэн бодис	Цэвээн, Канташкеев, Санжин

Бага сургуулиуд:

1921-1926 онд Оюунтүлхүүр, “Зурхайн бодлогын бичиг”, “Ертөнцийн байдал”, “Монгол үсгийн цагаан толгой”, “Балар цагийн түүх” зэрэг бүгд 23 төрлийн ном, сурах бичгийг тус бүрийг 1000-1500 хувь хэвлэн тараасан байна.

Тэр үед орон нутагт гэгээрлийн ажлыг удирдах төрийн байгууллага байгуулагдаж гэгээрлийн ажлыг хөгжүүлэх чухал арга хэмжээнүүдийг авч байлаа.

• 1926 оны 6 дугаар сард Хан Хэнтий уулын аймгийн сургуулийн багш нарын II их хурал болж сургуулийн цөөн жилийн ажлын туршлагаа ярилцаж байсан байна.
• Энэ хуралд монгол бичгийн нэрт эрдэмтэн С.Шагж нар оролцож байжээ. Гэгээрлийн яамнаас 1926 онд гаргасан нийт бага сургуулиудын дөрвөн жилд үзэх хичээлийн программд одоо ч хэрэгтэй сонин санаа их байгаагаас товч танилцуулъя.

Монгол орон нутгийн байдлын хичээлд: Сургуулиас гадагш зугаацахаар явж, юм үзэж, өвс ногоо, ургамал, чулууны нэрийг хэлж өгнө, өвс ногоо хавар хэдийд ургаж дэлгэрэх, ямар өвс ургамлыг ямар мал хэдийд иддэгийг таниулах, харьяат хот буюу сургуулийн орчин тойрон хэсэг газрыг барагцаалан хэмжээлж зургийг нь зурж сургах...

• харьяат аймаг хошууны газар ямар ямар зүйлийн хүнд тустай, хортой ургамал амьтан байх, тэдгээр бөгөөс хаа хэрхэн амьдрах тухай /мэдүүлэх/ гэх одоо ч ач холбогдол нь буураагүй чухал утга санааг агуулсан байна.

1930-аад оны эхэн үед бага дунд сургуулийн сурах бичиг олныг хэвлэн гаргажээ. Жишээлбэл:1933 онд

Ишдоржийн орчуулгаар 1932 онд байгалийн шинжлэл /амьтны аймаг/, /хий, ус, шороо, гурван махбод/, /ургамлын аймаг/, /хүмүүний биеийн байдал/, /амьтны аймаг дорд дэвтэр/ гэж таван дэвтэр

Гонгоржавын орчуулга “химийн ухаан”, монгол хэлний яруу найруулга, Далхжавын “Унших дэвтэр”, Ишдоржийн тооны ухааны товч тайлбар, Ц.Цэвэгжавын газарзүйн ном, физикийн дэвтэр

Эрдэнэбатуханы дэлхийн ерөнхий байдал, орос хэл сурах дэвтэр зэрэг олон арван номыг 10000 хүртэл хувиар хэвлэсний дотор зарим номыг латин үсгээр хэвлэн гаргасан байна.

Багшийн сургуулийн байгалийн ухааны хичээлийн түүхэн тойм

Он	Хичээлийн нэр	Багшийн нэр
1935	Физик, хими, түмэн бодис, дэлхий	Буддарь, Намжил, Өлзий, Байгаль, Батсүх
1938	Байгалийн шинжлэл, заах аргууд /дэлхий, байгаль/ , хувилахуйн ухаан, хими, физик, дэлхийн байдал, туршлагын ажил, сургуулийн аж ахуй
1939	хэл-түүх, тоо-физик, байгаль-газар зүй, орос хэлний багш мэргэжлээр төгсгөж байв.
1940	Дэлхийн байдал, байгаль шинжлэл, хувилахуй ухаан, физик, дэлхийн байдал заах арга, байгалийн шинжлэл заах арга, туршлагын хичээл, сургуулийн аж ахуй Тоо-физик /12/, хими-байгаль /14/, бага ангийг /42/, бага ангийн курсийг /512/ төгсөв.	Д.А.Шишкинская-хими, А.С.Карбенков , Хашганова–г/зүй, Шатская, Марьсов-биологи, Ишхонова ХАА, М.Насанбуян 1947
1948	Астрономи, байгалийн ухаан, амьтан судлал, хими	Э.Раднаа, Дунгаржид, Ломбодорж, Жамсран, Балдан
1949	Амьтан судлал, хими биологи, газар зүй Тоо-физик, байгаль дэлхий, хэл-уран зохиол, хими-биологи гэсэн 4 салбартай.	Жамсран, Балдан, Дэлгэрсүрэн

Эргэцүүлэх асуулт

1. Ишдоржийн багшийн 1929 онд байгалийн шинжлэлийн сурах бичигт буй “хий, ус, шороо, гурван махбод” бүлэг сэдэв орчин үеийн хүн байгаль хичээлийн ямар бүлэг сэдэв вэ?
2. Монгол орон нутгийн байдлын хичээлийн чадвар: “Сургуулиас гадагш зугаацахаар явж, юм үзэж, өвс ногоо, ургамал, чулууны нэрийг хэлж өгнө, өвс ногоо хавар хэдийд ургаж дэлгэрэх, ямар өвс ургамлыг ямар мал хэдийд иддэгийг таниулах, харьяат хот буюу сургуулийн орчин тойрон хэсэг газрыг барагцаалан хэмжээлж зургийг нь зурж сургах...” гэсэн 1926 онд дэвшүүлж байсан чадварууд 2019 оны бага боловсролын сайжруулсан хөтөлбөрт төсөөтэй чадварууд байна уу?

7.4.3.Суралцагчийн оролцоонд суурилсан бүтээлч арга зүй

Шинжлэн судлах арга зүй нь байгаль ертөнцийг судалж, өөрийн ажиглалт, сорил туршилт, эрэл хайгуул болон эрдэмтдийн бүтээл зэргээс олон арга замаар олж авсан нотолгоонд үндэслэн тайлбар санал болгох олон янзын арга замыг агуулдаг. Байгалийн ухааны сургалтад түгээмэл хэрэглэдэг энэхүү арга зүй нь суралцагчдад эрэл хайгуулаар мэдлэг, ур чадвар, дадал улмаар шинжлэх ухаанч арга барил хэвшүүлэх зорилготой.

Байгалийн ухааны аливаа асуулт, асуудалтай тулгарсан үед:

• Таамаглал дэвшүүлэх
• Ажлын төлөвлөгөө гаргах
• Төлөвлөсний дагуу гүйцэтгэх
• Мэдээллээ боловсруулах
• Дүгнэлт гаргах зэрэг алхмуудаар асуултынхаа хариулт, асуудлынхаа шийдлийг олох нь шинжлэх ухааны үүднээс хандаж, шинжлэх ухаанч арга барил эзэмших суурийг тавьдаг.

Шинжлэн судлах үйл	Чиглүүлэг
Таамаглал дэвшүүлэх	Тулгарсан асуултад өөрийн өнцгөөс бодож, эргэцүүлэн хариулах
Ажлын төлөвлөгөө гаргах	Холбогдох ажиглалт, сорил туршилт хийх, мэдээлэл, эх сурвалж, ном бүтээл зэргийг судлах, мэргэжилтэнтэй уулзах гэх мэт
Төлөвлөсний дагуу гүйцэтгэх	Ажлын төлөвлөгөөний дагуу гүйцэтгэж, биелэлтийг тооцох, тулгарсан асуудлыг шийдэх арга замыг хайх, боломжуудыг тооцох, хэрэгжүүлэх
Мэдээллээ боловсруулах	Олж авсан өгөгдөл мэдээллүүдэд боловсруулалт хийх
Дүгнэлт	Олж авсан нотолгоонд тулгуурласан тулгарсан асуултын хариултыг олох буюу шинжлэх ухаанч дүгнэлт гаргах

Шинжлэх ухааны судалгаа нь үндсэн хоёр үүрэгтэй. Нэгдүгээрт, шинжлэх ухааны судалгаа практикт хэрхэн явагддаг тухай тайлбарыг өгдөг. Хоёрдугаарт, шинжлэх ухааны эрэл хайгуул яагаад үйл явцынхаа төгсгөлд жинхэнэ мэдлэгт хүрч амжилтад хүрдэг талаар тайлбар өгдөг. Шинжлэх ухааны эрэл хайгуул нь тодорхой дарааллаар хийгдэх ба өгөгдлийг таамаглах, ажиглах, турших, ангилах, хэмжих, тайлбарлах, дүн шинжилгээ хийх, дүгнэлт гаргах гэх мэт ур чадварыг хөгжүүлэхээс гадна шинжлэх ухааны мэдлэг, шүүн тунгаах сэтгэлгээ, шинжлэх ухааны үндэслэлтэй хослуулна.

Шинжлэн судлах асуултын жишээ:

• Шувуу яагаад өндгөө дардаг вэ?
• Сохор номин нүдтэй юу?
• Загас нүдээ аньдаг уу?
• Анааш яагаад урт хүзүүтэй вэ?
• Цагаан баавгай хаана амьдардаг вэ?
• Оцон шувуу хаана амьдардаг вэ?
• Солонгыг өрөө тасалгаанд үүсгэж болох уу?
• Халуун ба хүйтэн усны аль нь түрүүлж хөлдөж эхлэх вэ?
• Могой араг ястай юу?
• Могой хэлээрээ хатгадаг уу, шүдээрээ хатгадаг уу?
• Туйлын туяа гэж юу вэ?
• Улаан лооль жимс үү, хүнсний ногоо юу? гэх мэт

Үзэгдэлд суурилсан арга зүй

Үзэгдэлд суурилсан арга зүй (Phenomenon-Based Learning - PhBL) нь сурагчдыг бодит амьдралын үзэгдэл, үйл явдлуудыг судлах замаар хичээл хоорондын мэдлэгийг нэгтгэн ойлгоход чиглэсэн сургалтын арга зүй юм. Энэ арга зүй нь сурагчдын шинжлэн судлах, асуудал шийдвэрлэх, бүтээлч сэтгэлгээ болон хамтран ажиллах чадварыг хөгжүүлэхэд онцгой ач холбогдолтой.

Бага ангийн байгалийн ухааны хичээлд үзэгдэлд суурилсан арга зүйг хэрэглэх нь:

Үзэгдлийг сонгох: Сурагчдын өдөр тутмын амьдралд ойр, сонирхолтой, насны онцлогт тохирсон үзэгдлийг сонгох нь чухал. Жишээлбэл, цаг агаарын өөрчлөлт, улирлын онцлог, ургамал амьтны амьдралын мөчлөг зэрэг сэдвүүдийг авч болно.

Ажиглалт, асуулт тавих: Сурагчид сонгосон үзэгдлийг ажиглаж, "Яагаад навчнууд намар унадаг вэ?", "Бороо хэрхэн үүсдэг вэ?" гэх мэт асуултуудыг өөрсдөө гарган тавина. Энэ нь тэдний сонирхлыг өдөөж, шинжлэн судлах үйл ажиллагаанд хөтөлнө.

Судалгаа, туршилт хийх: Сурагчид багшийн удирдлага дор жижиг туршилт, судалгаа явуулж, өөрсдийн асуултад хариулахыг оролдоно. Жишээлбэл, ургамлын өсөлтөд гэрлийн нөлөөг судлахын тулд гэрэлтэй болон харанхуй орчинд ургамал ургуулж, ялгааг ажиглах туршилт хийж болно.

Мэдээлэл солилцох, хэлэлцэх: Судалгааны үр дүнгээ ангийнхантайгаа хуваалцаж, хэлэлцүүлэг өрнүүлнэ. Энэ нь сурагчдын харилцааны чадварыг дээшлүүлж, мэдлэгээ бататгахад тусална.

Дүгнэлт гаргах, хэрэглээнд нэвтрүүлэх: Сурагчид судалгааныхаа үр дүнд үндэслэн дүгнэлт гаргаж, олж авсан мэдлэгээ бодит амьдралд хэрхэн хэрэглэх талаар ярилцана. Жишээлбэл, ургамлын өсөлтөд гэрэл хэрхэн нөлөөлдгийг мэдсэнээр гэртээ ургамал ургуулахдаа анхаарах зүйлсийг ойлгоно.

Энэхүү арга зүйг хэрэгжүүлэхдээ багш нь чиглүүлэгчийн үүрэг гүйцэтгэж, сурагчдын сонирхлыг өдөөх, асуулт тавих, туршилт хийхэд нь дэмжлэг үзүүлнэ. Мөн хичээл хоорондын уялдаа холбоог хангаж, сурагчдын бүтээлч сэтгэлгээ, асуудал шийдвэрлэх чадварыг хөгжүүлэхэд анхаарах хэрэгтэй.

Асуулт, даалгавар

1. Үзэгдэлд суурилсан арга зүйг ашиглах үед сурагчдын шинжлэн судлах чадварыг хөгжүүлэхэд ямар төрлийн үзэгдлийг сонгох нь илүү тохиромжтой вэ?
2. Хэрэв сурагчид үзэгдлийн шалтгааныг буруу тайлбарлавал багш ямар арга хэмжээ авах ёстой вэ?
3. Байгалийн ухааны хичээлд үзэгдэлд суурилсан арга зүйг ашиглахад сурагчдын сонирхлыг хэрхэн татаж, идэвхжүүлэх вэ?

Эх сурвалжууд:

• Сурагч төвтэй, тэгш хамруулах, оролцоонд суурилсан бүтээлч арга зүй гарын авлага. (2021).
• ХХI зууны багшлахуй ба суралцахуйн чиг хандлага ном. (2022).
• Taylor, C. (2022). Phenomenon-Based Instruction in the Elementary Classroom: Impact on Student Engagement and Achievement in Science Content Learning (Doctoral dissertation, Boise State University).
• Jongyung, T. (2025). Approaches and Techniques of Phenomenon-Based Learning: PheBL. Journal of Education and Learning Studies, 2(1).
• Isnawati, I., & Ismail, I. (2022). Analysis Scopus Article on Phenomenon-based Learning Through Bibliometric Analysis. KnE Social Sciences, 6(2), 1-12.

Төсөлд суурилсан арга зүй

Төсөлд суурилсан сургалтын арга зүй (Project-Based Learning - PBL) нь суралцагчдыг бодит амьдралын асуудал, асуулт, бэрхшээлийг урт хугацааны туршид судалж, шийдвэрлэх замаар мэдлэг, ур чадвар эзэмшихэд чиглэсэн сургалтын арга юм. Энэ арга зүй нь суралцагчдын идэвхтэй оролцоо, хамтын ажиллагаа, шүүмжлэлт сэтгэлгээ, бүтээлч байдал, асуудал шийдвэрлэх чадварыг хөгжүүлэхэд онцгой ач холбогдолтой.

Төсөлд суурилсан сургалтын онцлог:

1. Бодит амьдралтай холбоотой байдал: Суралцагчид бодит амьдралд тулгардаг асуудал, сорилтуудыг шийдвэрлэх төслүүд дээр ажиллаж, онолын мэдлэгээ практикт хэрэгжүүлдэг.
2. Суралцагч төвтэй байдал: Суралцагчид төслийн үйл ажиллагааг төлөвлөх, хэрэгжүүлэх, үнэлэх үйл явцад идэвхтэй оролцож, өөрсдийн суралцах үйл явцыг удирддаг.
3. Хамтын ажиллагаа: Төслийн ажлыг багийн хэлбэрээр гүйцэтгэх нь суралцагчдын харилцааны чадвар, багаар ажиллах ур чадварыг дээшлүүлдэг.
4. Салбар хоорондын уялдаа: Төслүүд нь олон төрлийн хичээл, сэдвийг нэгтгэн, суралцагчдыг өргөн хүрээний мэдлэг эзэмшихэд дэмжлэг үзүүлдэг.
5. Урт хугацааны үйл явц: Төслийн ажлууд нь ихэвчлэн хэдэн долоо хоногоос хэдэн сарын хугацаанд үргэлжилж, суралцагчдад сэдвийг гүнзгийрүүлэн судлах боломжийг олгодог.

Төсөлд суурилсан сургалтын үе шат:

1. Төслийн сэдэв сонгох: Суралцагчид болон багш хамтран сонирхолтой, ач холбогдолтой сэдвийг сонгож, төслийн зорилгоо тодорхойлно.
2. Төлөвлөлт: Төслийн үйл ажиллагааны төлөвлөгөө боловсруулж, үүрэг хариуцлагаа хуваарилна.
3. Судалгаа, мэдээлэл цуглуулах: Суралцагчид сонгосон сэдвийнхээ талаар мэдээлэл цуглуулж, судалгаа хийдэг.
4. Бүтээлч үйл ажиллагаа: Цуглуулсан мэдээлэлдээ үндэслэн шийдэл боловсруулах, бүтээгдэхүүн бүтээх, туршилт хийх зэрэг үйл ажиллагааг гүйцэтгэнэ.
5. Танилцуулга: Төслийн үр дүнгээ анги хамт олон, багш, эцэг эх болон бусад сонирхогч талуудад танилцуулж, тайлагнана.
6. Эргэцүүлэл, үнэлгээ: Төслийн үйл явц, үр дүнг эргэцүүлэн бодож, давуу болон сул талуудыг тодорхойлон, цаашдын сайжруулалтын талаар хэлэлцэнэ.

Төсөлд суурилсан сургалтын давуу талууд:

• Идэвхтэй суралцахуй: Суралцагчид өөрсдөө асуудлыг шийдвэрлэх үйл явцад оролцсоноор мэдлэгээ бататгаж, ур чадвараа хөгжүүлдэг.
• Бүтээлч сэтгэлгээ хөгжүүлэх: Төслийн ажлууд нь суралцагчдаас шинэлэг санаа, шийдэл гаргахыг шаарддаг тул бүтээлч байдлыг дэмждэг.
• Харилцааны чадвар дээшлүүлэх: Багийн ажил, танилцуулга хийх зэрэг үйл ажиллагаа нь суралцагчдын харилцааны чадварыг сайжруулдаг.
• Асуудал шийдвэрлэх чадвар хөгжүүлэх: Бодит амьдралын асуудлуудыг шийдвэрлэх явцад суралцагчид асуудалд шүүмжлэлтэй хандах, шийдэл олох чадвараа дээшлүүлдэг.

Асуулт, даалгавар

1. Төсөлд суурилсан сургалтын үед сурагчид өөрсдөө асуудлаа тодорхойлж, шийдэл боловсруулахдаа ямар ур чадварыг хамгийн их хөгжүүлдэг вэ?
2. Төсөл хэрэгжүүлэх явцад сурагчдын суралцах үйл явцыг хэрхэн үнэлэх нь илүү үр дүнтэй вэ?
3. Бага ангийн байгалийн ухааны хичээлд төсөлд суурилсан арга зүйг хэрэглэхэд тулгарч болох сорилтууд юу вэ?

Эх сурвалжууд:

• Kurt, G., & Akoglu, K. (2023). Project-based learning in science education: A comprehensive literature review. Interdisciplinary Journal of Environmental and Science Education, 19(3), e2311.
• Krajcik, J., Schneider, B., Miller, E. A., Chen, I.-C., Bradford, L., Baker, Q., Bartz, K., Miller, C., Li, T., Codere, S., & Peek-Brown, D. (2023). Assessing the effect of project-based learning on science learning in elementary schools. American Educational Research Journal, 60(1), 70–102.
• Krajcik, J. S., & Czerniak, C. M. (2018). Teaching science in elementary and middle school: A project-based learning approach. Routledge.

Даалгаварт суурилсан арга зүй

Даалгаварт суурилсан сургалтын арга зүй (Task-Based Learning - TBL) нь суралцагчдыг бодит амьдралын нөхцөл байдалд тулгуурласан даалгавруудыг гүйцэтгэх замаар хэлний мэдлэг, ур чадвараа хөгжүүлэхэд чиглэсэн сургалтын арга юм. Энэхүү арга зүй нь суралцагчдыг идэвхтэй оролцоонд уриалж, харилцааны чадварыг сайжруулахад онцгой ач холбогдолтой.

Даалгаварт суурилсан сургалтын үндсэн үе шатууд:

1. Даалгаврын өмнөх шат (Pre-task): Багш суралцагчдад даалгаврын сэдэв, зорилгыг танилцуулж, шаардлагатай үг хэллэг, хэлзүйн бүтэцтэй танилцуулна. Энэ шатанд суралцагчдын сонирхлыг өдөөж, даалгаврыг гүйцэтгэхэд бэлтгэнэ.
2. Даалгаврын үе шат (During-task): Суралцагчид багшийн өгсөн даалгаврыг бие даан эсвэл багийн хэлбэрээр гүйцэтгэнэ. Энэ үе шатанд багш ажиглагч, дэмжигчийн үүрэг гүйцэтгэж, шаардлагатай үед зөвлөгөө өгнө.
3. Даалгаврын дараах шат (Post-task): Суралцагчид даалгаврынхаа үр дүнг танилцуулж, хэлэлцүүлэг өрнүүлнэ. Багш энэ шатанд хэлзүйн алдаа засах, нэмэлт тайлбар өгөх зэрэг үйл ажиллагааг зохион байгуулна.

Даалгаварт суурилсан сургалтын давуу талууд:

• Бодит хэрэглээ: Суралцагчид бодит амьдралд тулгардаг нөхцөл байдалд хэлээ ашиглах боломжтой болсноор хэлний мэдлэгээ практикт хэрэгжүүлдэг.
• Идэвхтэй оролцоо: Даалгаврууд нь суралцагчдын сонирхлыг татаж, тэднийг идэвхтэй суралцах үйл явцад оролцуулдаг.
• Харилцааны чадвар хөгжүүлэх: Багийн ажил, хэлэлцүүлэг зэрэг үйл ажиллагаа нь суралцагчдын харилцааны чадварыг сайжруулдаг.

Асуулт, даалгавар

1. Сурагчдад даалгавар гүйцэтгүүлэхээс өмнө багш ямар урьдчилсан тайлбар, чиглэл өгөх хэрэгтэй вэ?
2. Даалгаврын гүйцэтгэлийн явцад сурагчид алдаа гаргавал багш шууд засах ёстой юу, эсвэл ажлаа дуусгасны дараа тайлбарлах нь зөв үү?
3. Байгалийн ухааны хичээлд бодит амьдралтай холбоотой даалгавар өгөх нь сурагчдын ойлголтыг хэрхэн бататгах боломжтой вэ?

Эх сурвалжууд:

• Г. Халиун. (2021). Даалгаварт суурилсан сургалтын арга зүй. Сурагч төвтэй, тэгш хамруулах, оролцоонд суурилсан бүтээлч арга зүй гарын авлага.
• https://bolovsrolsudlal.mn/index.php/home/article/view/77
• Willis, J. (1996). A Framework for Task-Based Learning. Longman.
• Ellis, R. (2003). Task-Based Language Learning and Teaching. Oxford University Press.
• Nunan, D. (2004). Task-Based Language Teaching. Cambridge University Press.

7.4.4.Ташаа ойлголт

Ташаа ойлголт гэдэг нь хүн аливаа үзэгдэл, ойлголт, баримтыг буруу эсвэл дутуу ойлгосон, шинжлэх ухааны үндэслэлтэй мэдлэгтэй зөрчилдөх байдлыг хэлнэ. Энэ нь ихэвчлэн өдөр тутмын амьдралын ажиглалт, буруу мэдээлэл, соёлын итгэл үнэмшил, хязгаарлагдмал мэдлэгээс үүдэлтэй байдаг. Ташаа ойлголт нь зөв ойлголтыг бий болгоход саад учруулж, суралцах үйл явцыг хүндрүүлдэг.

Ташаа ойлголт үүсэх шалтгаанууд:

1. Өдөр тутмын ажиглалт:
   o Хүмүүс ажигласнаа өөрсдийн туршлага дээр тулгуурлан тайлбарлахдаа буруу дүгнэлт хийх нь элбэг. Жишээлбэл, нар "тэнгэрт хөдөлж" байгаа мэт харагддаг тул хүмүүс дэлхий хөдөлдөг гэдгийг ойлгоход хэцүү байдаг.
2. Буруу мэдээлэл:
   o Хэвлэл мэдээлэл, интернэт, ном зохиол болон бусад эх сурвалжаас ирсэн буруу мэдээлэл ташаа ойлголтыг бий болгодог.
3. Оюун санааны төсөөлөл:
   o Хүүхдүүд болон насанд хүрэгчид өөрсдийн мэдлэгийн түвшиндээ тулгуурлан бодит байдлыг өөрсдөө тайлбарлахыг оролддог. Жишээлбэл, сарны хэлбэр өөрчлөгддөг нь дэлхийн сүүдэрээс болж байна гэж бодох нь түгээмэл ташаа ойлголт юм.
4. Сургалтын арга зүйн алдаа:
   o Багшийн заах арга зүй, сургалтын хэрэглэгдэхүүн дутуу, буруу тайлбар өгвөл сурагчид буруу ойлголттой болох эрсдэлтэй.

Ташаа ойлголтын үр дагавар:

• Шинэ мэдлэгийг зөв ойлгоход саад болдог.
• Суралцах үйл явцыг удаашруулдаг.
• Идэвхтэй суралцах хүсэл сонирхлыг бууруулдаг.

Ташаа ойлголтыг залруулах арга замууд:

1. Шинжлэх ухааны нотолгоонд тулгуурлах:
   Туршилт, ажиглалт, баримт дээр суурилсан сургалт нь буруу ойлголтыг засахад үр дүнтэй.
2. Асуудал дэвшүүлэн хэлэлцэх:
   Сурагчдыг өөрийнхөө ойлголтыг тайлбарлах, хамгаалах, бусадтай харьцуулах боломж олгох.
3. Тодорхой, ойлгомжтой тайлбар өгөх:
   Багш нар ойлголтыг энгийн, насанд тохирсон хэлбэрээр тайлбарлах нь зүйтэй.
4. Харилцан яриа, асуулт хариулт:
   Сурагчдын буруу ойлголтыг эрт таньж, үнэн зөв ойлголтыг бүрдүүлэхэд чиглүүлэх нь чухал.

Асуулт, даалгавар

1. Сурагчид улирлын өөрчлөлтийг дэлхий нарнаас холдох, ойртохоос шалтгаалдаг гэж ташаа ойлговол энэ ойлголтыг хэрхэн зөв болгох вэ?
2. Хэрэв сурагч нар зөвхөн гэрэлтэй биет л сүүдэр үүсгэдэг гэж ойлгож байвал багш үүнийг засах ямар туршилт зохион байгуулж болох вэ?
3. Ташаа ойлголтыг эрт таньж, засахад багшийн зүгээс ямар аргууд хамгийн үр дүнтэй байдаг вэ?

Эх сурвалжууд:

• Driver, R., Squires, A., Rushworth, P., & Wood-Robinson, V. (2014). Making sense of secondary science: Research into children's ideas. Routledge.
• Vosniadou, S. (2013). International handbook of research on conceptual change. Routledge.
• Nussbaum, J., & Novak, J. (2011). Alternative frameworks, conceptual conflict and accommodation: Toward a principled teaching strategy. Instructional Science, 11(3), 183-200.
• Clement, J. (2013). Students' preconceptions in introductory mechanics. American Journal of Physics, 50(1), 66-71.

7.4.5 Ажиглалт, сорил туршилт хийх арга зүй

Суралцахуйн зорилт

• Туршилтын багаж ашиглах, гарын доорх материал ашиглан бүтээх
• Туршилтын ажлын хуудас боловсруулах

Бага ангийн байгалийн ухааны хичээлд ажиглалт болон сорил туршилт хийх арга зүйг хэрэглэх нь сурагчдын шинжлэх ухаанч сэтгэлгээг хөгжүүлэх, мэдлэгийг бататгах, сонирхлыг нэмэгдүүлэхэд чухал үүрэгтэй.

Ажиглалт хийх арга зүй:

Ажиглалт нь сурагчдыг байгаль орчин, эргэн тойрон дахь үзэгдэл, үйл явцыг анхааралтай ажиглаж, мэдээлэл цуглуулахад сургадаг. Энэ нь тэдний танин мэдэхүйн чадварыг дээшлүүлж, шинжлэх ухааны үндэслэлтэй дүгнэлт хийхэд тусалдаг.

Сорил туршилт хийх арга зүй:

Сорил туршилт нь сурагчдад онолын мэдлэгийг практикт хэрэгжүүлэх, туршилтаар дамжуулан ойлголтоо бататгах боломжийг олгодог. Энэ арга зүй нь сурагчдын асуудал шийдвэрлэх, шүүмжлэлтэй сэтгэлгээ, багаар ажиллах чадварыг хөгжүүлдэг.

Бага ангийн байгалийн ухааны хичээлд хэрэглэх нь:

• Хичээлийн төлөвлөлт: Багш нар хичээлийн төлөвлөгөөндөө ажиглалт болон сорил туршилтыг оновчтойгоор тусгаж, сурагчдын нас, сэтгэхүйн онцлогт тохируулан зохион байгуулах хэрэгтэй.
• Хэрэглэгдэхүүн бэлтгэх: Туршилт, ажиглалтад шаардлагатай энгийн багаж хэрэгсэл, материалуудыг урьдчилан бэлтгэж, аюулгүй ажиллагааны зааварчилгааг сайтар өгөх нь чухал.
• Сурагчдын оролцоо: Сурагчдыг идэвхтэй оролцуулж, өөрсдөө туршилт хийх, ажиглалт явуулах боломжийг олгох нь тэдний суралцах үйл явцыг дэмжинэ.
• Үнэлгээ, дүгнэлт:Туршилт, ажиглалтаас гарсан үр дүнг хамтдаа хэлэлцэж, дүгнэлт гаргах замаар сурагчдын ойлголтыг бататгах, алдааг залруулах боломжтой.

Жишээ нь:

Цаг агаар ба уур амьсгал агуулгын хүрээнд дараах хэрэглэгдэхүүнийг гарын доорх материал ашиглан хийж болно.

• Цахим хэрэглэгдэхүүн боловсруулах арга зүй
  • Бага ангийн сурагчдад зориулсан нээлттэй эх ашиглах нь /youtube, phet, …/
  • Ажлын хуудас, зураг, хөдөлгөөнт дүрс, видео боловсруулах

Аюулгүй ажиллагааны дүрэм

Аюулгүй ажиллагааны дүрэм гэдэг нь хувь хүн, эд хөрөнгө, хүрээлэн буй орчныг болзошгүй аюул, осол, гэмтлээс хамгаалахад чиглэсэн тогтоосон заавар, дүрэм, зарчмуудыг хэлнэ.

Ажлын байр, сургууль, лаборатори, олон нийтийн газар гэх мэт янз бүрийн орчинд эрсдэлийг бууруулах, аюулгүй, хариуцлагатай зан үйлийг төлөвшүүлэх зорилгоор эдгээр дүрмийг мөрддөг. Аюулгүй ажиллагааны дүрэм нь осол, гэмтэл бэртлээс урьдчилан сэргийлэхэд зайлшгүй шаардлагатай бөгөөд ихэвчлэн тоног, төхөөрөмж, машин механизм ашиглах, аюултай материалтай харьцах, галын аюулгүй байдал, замын хөдөлгөөний дүрэм гэх мэт олон төрлийн үйл ажиллагаа, нөхцөл байдлыг хамардаг. Аюулгүй ажиллагааны дүрмийг дагаж мөрдөх нь хувь хүмүүсийн сайн сайхан байдал, олон нийт, байгууллагын аюулгүй байдлыг хангахад маш чухал юм. Энд дарж аюулгүй ажиллагааны дүрмийг дэлгэрэнгүй үзээрэй.

Видео 1. Туршилтын багаж, тоног төхөөрөмж

Видео 2. Туршилтын багаж, тоног төхөөрөмж, Микроскоп

Видео 4. Аюулгүй ажиллагааны дүрэм

Туршилтат хичээлд гарын доорх материал ашиглан хэрэглэгдэхүүн, багаж хэрэгсэл бүтээж хэрэглэх нь

Гарын доорх олдоц ихтэй материал ашиглан бага ангийн байгалийн ухааны туршилтат хичээлд хэрэглэгдэх хэрэглэгдэхүүн (багаж хэрэгсэл, тоног төхөөрөмж)-ийг бүтээх нь дараах ач холбогдолтой. Энд дарж дэлгэрэнгүй үзээрэй.

Видео 3. Гарын доорх материал ашиглан байгалийн үзэгдэл ажиглах сонирхолтой хэрэглэгдэхүүн бүтээх

Видео 5. Гарын доорх материал ашиглан салхины зүг чиг олох флюгер багаж бүтээх

Видео 6. Соронзны туршилтууд

Эргэцүүлэх асуулт:

1. Байгаль орчин дахь өөрчлөлтийг ажиглахад ямар мэдрэхүйг түлхүү ашиглах вэ?
2. Ажиглалтын үеэр мэдээллийг хэрхэн тэмдэглэж, хөтлөх нь илүү үр дүнтэй вэ?
3. Байгальд ажиглалт хийх үед ямар хүчин зүйлс ажиглалтыг гажуудуулж болох вэ?
4. Сурагчид байгалийн ухааны туршилт хийхдээ ямар үе шатыг дагаж мөрдөх ёстой вэ?
5. Туршилтын үр дүн буруу гарсан тохиолдолд ямар алхам хийх хэрэгтэй вэ?
6. Хичээл дээр энгийн сорил туршилт хийхэд ямар аюулгүй ажиллагааны дүрэм баримтлах ёстой вэ?
7. Бага ангийн сурагчид ажиглалт, туршилтын арга зүйг ашигласнаар ямар ур чадвар эзэмших вэ?
8. Байгалийн ухааны хичээл дээр туршилт хийх нь сурагчдын ойлголтыг хэрхэн бататгадаг вэ?
9. Ямар төрлийн ажиглалт, сорил туршилт бага ангийн хүүхдэд илүү тохиромжтой вэ?

Ажлын хуудас

Ажлын хуудас гэдэг нь тухайн сэдвийн талаарх мэдлэг, ойлголтыг бататгахад зориулагдсан ажлын хуваарь, гүйцэтгэх хугацаа, санамж, тусгай заавар зэргийг багтаасан тусгайлан бэлтгэсэн дасгалын хуудас. Тодорхой ажлын үйл явц, гүйцэтгэл, үр дүн зэргийг ажлын хуудсанд тэмдэглэж болно. Эдгээр нь ихэвчлэн дасгал даалгавар, ажиглалт туршилт, маягт, нягтлан бодох бүртгэл, бизнесийн гэх мэт олон хэлбэр, зориулалтаар боловсруулагдсан байдаг. Цаасан болон программ дээр суурилсан ажлын хуудсыг өргөн хэрэглэдэг. Тодорхой зорилго бүхий ажиглалт болон туршилтын дараалал, тусгай заавар зэргийг тусгасан, асуудал, санаа, үүнтэй төстэй зүйлсийг агуулсан хуудас юм. Мөн ажлын хуудсанд суралцагчдад зориулсан асуултууд, хариултыг бичих талбарыг тусгаж болно.

Нягтлан бодох бүртгэлийн хувьд ажлын хуудас гэдэг нь нягтлан бодогч мэдээллийг бүртгэх эсвэл тооцоо хийх боломжтой мөр, баганатай байдаг байна.

Байгалийн ухааны сургалтад түгээмэл хэрэглэгдэх ажлын хуудасны хэлбэр, түлхүүр үгийг доор дурдав.

Байгалийн ухааны сургалтад түгээмэл ашиглагддаг ажлын хуудасны зарим хэлбэрүүд:

• Ажиглалт тэмдэглэх
• Туршилтын багаж, хэрэгсэл бүтээх
• Туршилтын үр дүн тэмдэглэх
• Дасгал, даалгавар гүйцэтгэх гэх мэт

Ажлын хуудсанд түгээмэл ашиглагдах түлхүүр үг:

• Worksheet – Ажлын хуудас
• Purpose - Зорилго
• Question - Асуулт
• Hypothesis - Таамаглал
• Materials - Хэрэглэгдэхүүн
• Safety rules - Аюулгүй ажиллагааны дүрэм
• Procedure - Үйл ажиллагааны дараалал
• Result- Үр дүн
• Conclusion – Дүгнэлт

Даалгавар

Дээрх түлхүүр үгийг ашиглан интернэтээс хайлт хийж, жишээ ажлын хуудасны загвартай танилцаж болно. Ажлын хуудасны нийтлэг болон онцлог зүйлийг харьцуулаарай.

Туршилтын ажлын хуудас:

Ажлын ном нь ажлын хуудасны цуглуулгын бүрдэл байх боломжтой. Бага ангийн 1, 2 дугаар ангийн сурагч тэдгээрийн эцэг эх, асран хамгаалагчид, багш нарын хэрэглээнд зориулан боловсруулагдсан “Дасгал ажлын дэвтэр”-тэй дараах линкээр орж танилцаж, түүнд түшиглэн ажлын хуудас боловсруулах боломжтой.

Дасгал ажлын дэвтэр 1

Дасгал ажлын дэвтэр 2

7.4.6 Бага боловсролын байгалийн ухааны үнэлгээний арга зүй

Суралцахуйн зорилт

• Үнэлгээний хэлбэр төрлийг бага боловсролын байгалийн ухааны сургалтад хэрэглэх чадвар эзэмших
• Бага боловсролын байгалийн ухааны үнэлгээний нэгж, суралцахуйн үр дүн, шалгуур, гүйцэтгэлийн түвшинтэй танилцах
• Бага боловсролын үнэлгээний шалгуурт нийцсэн даалгавар, блюпринт боловсруулах арга зүй эзэмших
• Үнэлгээний даалгаврын гүйцэтгэлд суурилсан шинжилгээ хийх

Бага боловсролын байгалийн ухааны хичээлд үнэлгээний арга зүйг оновчтой хэрэглэх нь сурагчдын мэдлэг, чадвар, хандлагыг бодитой тодорхойлох, цаашдын сургалтын үйл ажиллагааг төлөвлөхөд чухал үүрэгтэй. Үнэлгээ нь суралцахуйн үйл явцын салшгүй хэсэг бөгөөд сургалтын чанарыг дээшлүүлэх, сурагчдын ахицыг хянах, багшийн арга зүйг сайжруулахад чиглэгддэг.

Үнэлгээний шалгуур:

Үнэлгээ хийхдээ тодорхой, хэмжигдэхүйц шалгуур тогтоох нь чухал. Эдгээр шалгуур нь сурагчдын гүйцэтгэлийг бодитой, шударга үнэлэх үндэс болдог. Жишээлбэл, байгалийн ухааны хичээлд дараах шалгуурыг ашиглаж болно:

• Мэдлэгийн түвшин: Сурагч тухайн сэдвийн үндсэн ойлголт, нэр томьёог зөв ойлгож, тайлбарлаж чадаж байгаа эсэх.
• Чадварын түвшин: Сурагч туршилт, ажиглалт хийх, мэдээлэл цуглуулах, дүгнэлт гаргах чадвартай эсэх.
• Хандлага: Сурагчийн суралцах идэвх, хамтын ажиллагаа, хариуцлагатай байдал.

Ерөнхий боловсролын сургуулийн суралцагчийн болон боловсролын чанарын үнэлгээний журмын дагуу суралцагчийн эзэмшсэн мэдлэг, чадварын ахиц, амжилтыг 1-3 дугаар ангид үгэн үнэлгээгээр үнэлнэ.

Эзэмшсэн мэдлэг, чадварын ахиц, амжилтын түвшин	Үгэн үнэлгээ
Дээд	Маш сайн
Дунджаас дээгүүр	Хангалттай
Дундаж	Сайжирч байгаа
Дунджаас доогуур	Анхаарах шаардлагатай

Бага ангийн сурагчид байгалийн ухааны хичээлээр чанарын үнэлгээний болон улсын шалгалт өгдөг. Мөн олон улсад бага боловсролын математик болон байгалийн ухааны хичээлээр шалгалт авч, тэдгээрийг эрэмбэлдэг.

Үнэлгээ	PISA	TIMSS	PIRLS
Үнэлгээний бүтэн нэр	Олон улсын сурагчдын үнэлгээний программ	Олон улсын математик, байгалийн ухааны судалгааны чиг хандлага	Олон улсын уншлага, бичиг үсгийн судалгааны үйл явц
Шалгах үнэлгээ	Уншлага, математик, байгалийн ухаан, асуудал шийдвэрлэх	Математик болон байгаль нийгэм	Уншлага
Нас	15	10 ба 14	10
Анги	9	4 ба 8	4
Давтамж	2000 оноос 3 жил тутам	1995 оноос 4 жил тутам	2001 оноос 5 жил тутам
Фокус	Чадварт суурилсан	Хөтөлбөрт суурилсан	Хөтөлбөрт суурилсан
Зохион байгуулагч	Эдийн засгийн хамтын ажиллагаа болон хөгжлийн төлөөх байгууллага	Боловсролын амжилтын үнэлгээний төлөөх олон улсын нийгэмлэг	Боловсролын амжилтын үнэлгээний төлөөх олон улсын нийгэмлэг
Хамрагдах улс	2012 онд 65 улс	2011 онд 66 улс + 14	2011 онд 55 улс + 7
Тест гүйцэтгэх хугацаа	120 минут + 15 мин үндсэн асуулга	4-р анги 72 мин, 8-р анги 90 мин + 15 мин үндсэн асуулга	80 минут + 15 мин үндсэн асуулга
Үнэлүүлсэн суралцагчдын тоо	Улс бүрээс 5000-аас дээш	Сүүлд улс бүрээс 4000-аас дээш	Улс бүрээс 3500-4000

Эргэцүүлэх асуулт:

1. Бага ангийн байгалийн ухааны хичээлд үнэлгээ хийхдээ мэдлэг, чадвар, хандлагын аль талд илүү анхаарах нь зүйтэй вэ?
2. Хичээлийн практик туршилт, төсөл дээр суурилсан үнэлгээ хийхдээ ямар шалгуур баримтлах хэрэгтэй вэ?
3. Сурагчдын үнэлгээг эцэг эхэд хэрхэн ойлгомжтой, үр дүнтэйгээр танилцуулах вэ?